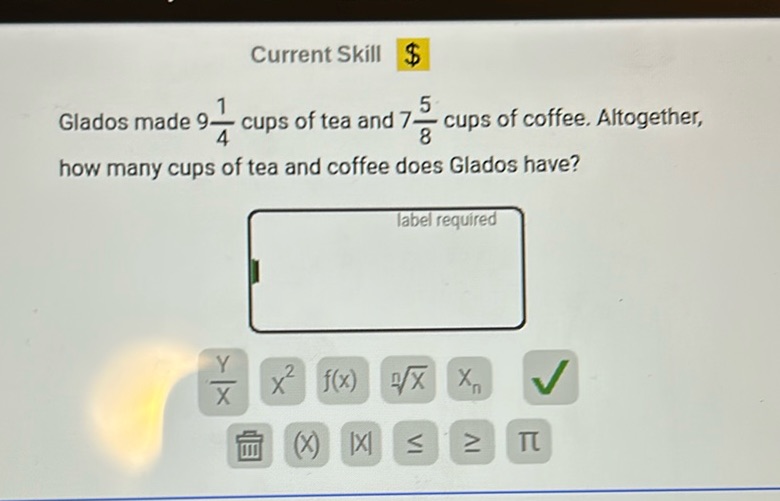
Question: Current Skill $\$\$ Glados made 9\frac{1}{4} cups of tea and 7\frac{5}{8} cups of coffee…

Current Skill $\$\$ Glados made 9\frac{1}{4} cups of tea and 7\frac{5}{8} cups of coffee. Altogether, how many cups of tea and coffee does Glados have?

Solution

Glados made \(9\frac{1}{4}\) cups of tea and \(7\frac{5}{8}\) cups of coffee. We need to find out how many cups of tea and coffee Glados has altogether. First, convert the mixed numbers to improper fractions. For \(9\frac{1}{4}\): \(9\frac{1}{4} = \frac{9 \times 4 + 1}{4} = \frac{36 + 1}{4} = \frac{37}{4}\) For \(7\frac{5}{8}\): \(7\frac{5}{8} = \frac{7 \times 8 + 5}{8} = \frac{56 + 5}{8} = \frac{61}{8}\) Now, add the two improper fractions: Find the common denominator, which is 8. Convert \(\frac{37}{4}\) to the equivalent fraction with a denominator of 8: \(\frac{37}{4} = \frac{37 \times 2}{4 \times 2} = \frac{74}{8}\) Now add the fractions: \[ \frac{74}{8} + \frac{61}{8} = \frac{74 + 61}{8} = \frac{135}{8} \] Convert back to a mixed number: Divide 135 by 8: 135 ÷ 8 = 16 R7 So, \(\frac{135}{8} = 16\frac{7}{8}\) Glados has \(16\frac{7}{8}\) cups of tea and coffee altogether.