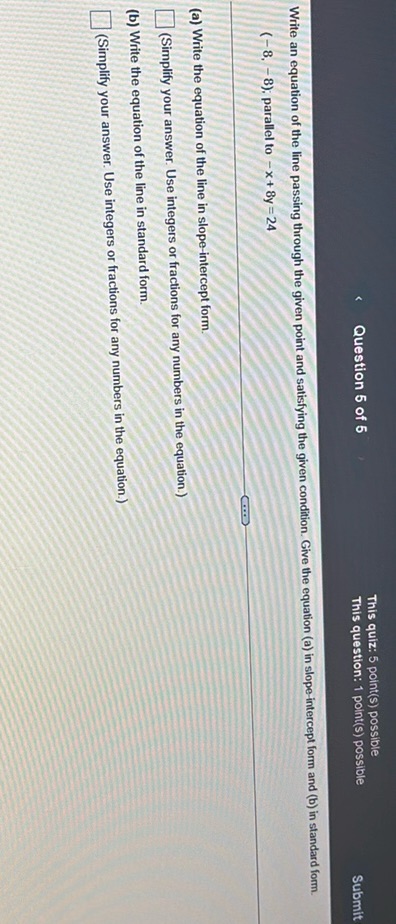
Question: Write an equation of the line passing through the given point and satisfying the given condition…

Write an equation of the line passing through the given point and satisfying the given condition. Give the equation (a) in slope-intercept form and (b) in standard form.

(a) Write the equation of the line in slope-intercept form. (-8, 9) parallel to \( x - 8y = 24 \)

(Simplify your answer. Use integers or fractions for any numbers in the equation.)

(b) Write the equation of the line in standard form. (Simplify your answer. Use integers or fractions for any numbers in the equation.)

Solution

Write an equation of the line passing through the given point and satisfying the given condition. The point is \( (8, -8) \) and the line is parallel to \( x + 8y = 24 \). Step 1: Find the slope of the given line. The equation of the line is \( x + 8y = 24 \). Convert it to slope-intercept form \( y = mx + b \). \[ 8y = -x + 24 \] \[ y = -\frac{1}{8}x + 3 \] The slope (\( m \)) of the line is \( -\frac{1}{8} \). Step 2: Use the point-slope form to write the equation of the line parallel to the given line and passing through \( (8, -8) \). The point-slope form is \( y - y_1 = m(x - x_1) \). Substitute \( m = -\frac{1}{8} \), \( x_1 = 8 \), and \( y_1 = -8 \). \[ y + 8 = -\frac{1}{8}(x - 8) \] Step 3: Simplify the equation. \[ y + 8 = -\frac{1}{8}x + 1 \] \[ y = -\frac{1}{8}x - 7 \] This is the slope-intercept form. Step 4: Convert this to standard form \( Ax + By = C \). Multiply the entire equation by 8 to eliminate fractions. \[ 8y = -x - 56 \] \[ x + 8y = -56 \] The standard form is \( x + 8y = -56 \).