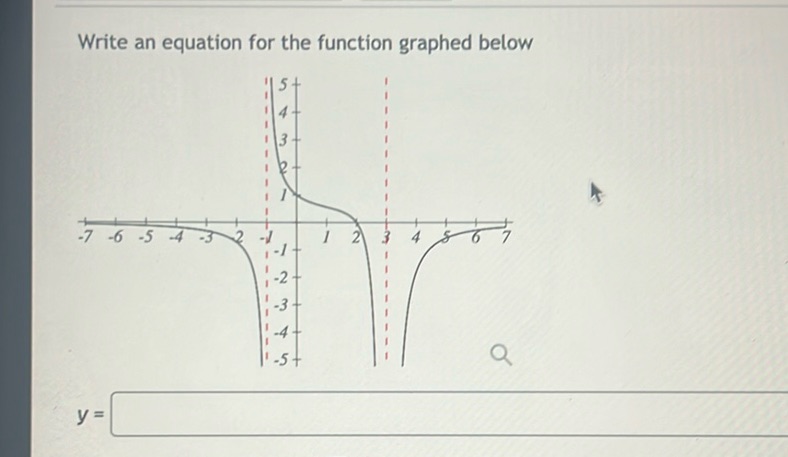
Question: Write an equation for the function graphed below \[ y = \frac{1}{x^2 - 4} \]

Write an equation for the function graphed below

\[ y = \frac{1}{x^2 - 4} \]

Solution

The graph shows a rational function with vertical asymptotes at \(x = 2\) and \(x = 3\), and a horizontal asymptote at \(y = 0\). The general form of a rational function with vertical asymptotes can be expressed as: \[ y = \frac{a}{(x - 2)(x - 3)} \] The function approaches zero as \(x\) goes to infinity, indicating there is no horizontal shift. The numerator needs to be a constant for the horizontal asymptote to be at \(y = 0\). Observing the behavior near the asymptotes and the origin, the function likely doesn’t have any additional linear or higher power terms in the numerator. Thus, the equation of the function is: \[ y = \frac{1}{(x - 2)(x - 3)} \]