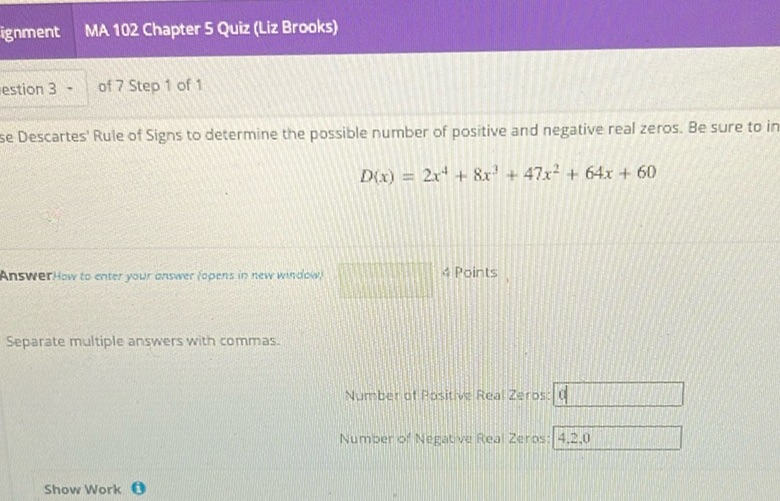
Question: Use Descartes’ Rule of Signs to determine the possible number of positive and negative real zeros…

Use Descartes’ Rule of Signs to determine the possible number of positive and negative real zeros. Be sure to include all possibilities.

\[ D(x) = 2x^4 + 8x^3 + 47x^2 + 64x + 60 \]

Number of Positive Real Zeros: 0

Number of Negative Real Zeros: 4, 2, 0

Solution

Let’s determine the possible number of positive and negative real zeros for the polynomial function: \[ D(x) = 2x^4 + 8x^3 + 47x^2 + 64x + 60 \] Step 1: Determine the Number of Positive Real Zeros To find the number of positive real zeros, we count the number of sign changes in \( D(x) \). \[ D(x) = 2x^4 + 8x^3 + 47x^2 + 64x + 60 \] All the coefficients are positive, so there are 0 sign changes. \[ \text{Number of positive real zeros} = 0 \] Step 2: Determine the Number of Negative Real Zeros To find the number of negative real zeros, we evaluate \( D(-x) \) and count the number of sign changes. \[ D(-x) = 2(-x)^4 + 8(-x)^3 + 47(-x)^2 + 64(-x) + 60 \] Simplifying: \[ D(-x) = 2x^4 - 8x^3 + 47x^2 - 64x + 60 \] Now, count the sign changes: - \( 2x^4 \) to \( -8x^3 \): 1 sign change - \( -8x^3 \) to \( 47x^2 \): 2 sign changes - \( 47x^2 \) to \( -64x \): 3 sign changes - \( -64x \) to \( 60 \): 4 sign changes According to Descartes’ Rule of Signs, the number of negative real zeros is equal to the number of sign changes or less by an even number. Therefore, the possible number of negative real zeros is 4, 2, or 0. \[ \text{Number of negative real zeros} = 4, \; 2, \; \text{or} \; 0 \] Final Answer: - Number of positive real zeros: \( 0 \) - Number of negative real zeros: \( 4, \; 2, \; \text{or} \; 0 \)