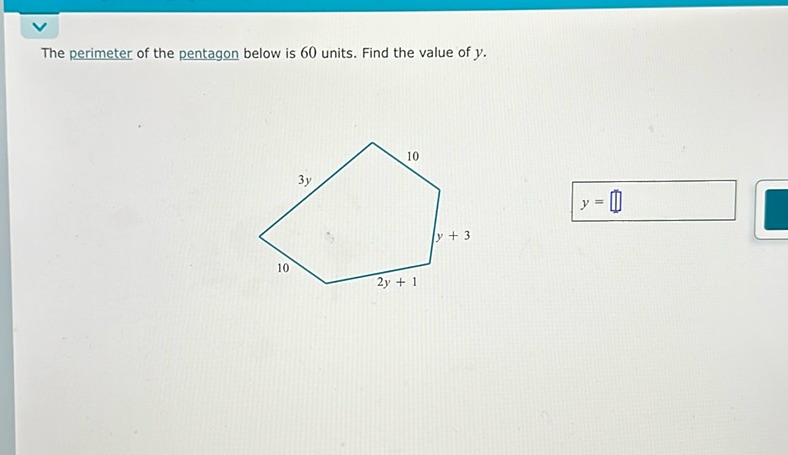
Question: The perimeter of the pentagon below is 60 units. Find the value of \( y \). \[…

The perimeter of the pentagon below is 60 units. Find the value of \( y \).

\[ \begin{array}{c} \text{3y} \\ \text{10} \\ \text{y + 3} \\ \text{2y + 1} \\ \text{10} \end{array} \]

\( y = \boxed{\phantom{0}} \)

Solution

To find the value of \( y \), we need to set up an equation for the perimeter of the pentagon. The perimeter is the sum of all the side lengths: \[ 3y + 10 + 10 + 2y + 1 + y + 3 = 60 \] Combine like terms: \[ 3y + 2y + y + 10 + 10 + 1 + 3 = 60 \] Simplify the equation: \[ 6y + 24 = 60 \] Subtract 24 from both sides: \[ 6y = 36 \] Divide by 6: \[ y = 6 \] The value of \( y \) is 6.