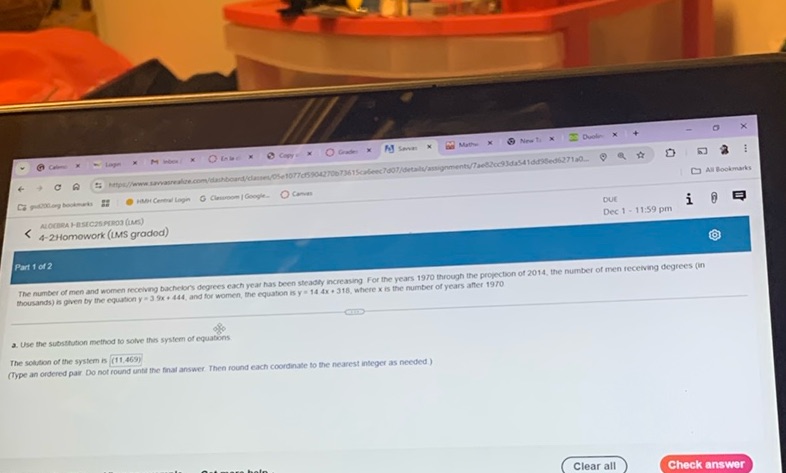
Question: The number of men and women receiving bachelor’s degrees each year has been steadily increasing…

The number of men and women receiving bachelor’s degrees each year has been steadily increasing. For the years 1970 through the projection of 2014, the number of men receiving degrees (in thousands) is given by the equation y = 3.9x + 444, and for women, the equation is y = 14.4x + 318, where x is the number of years after 1970.

Use the substitution method to solve this system of equations.

The solution of the system is (11, 469).

(Type an ordered pair. Do not round until the final answer. Then round each coordinate to the nearest integer as needed.)

Solution

First, set the two equations equal to each other since both equal \( y \): \[ 5x + 444 = 11.4x + 318 \] Next, subtract \( 5x \) from both sides of the equation: \[ 444 = 6.4x + 318 \] Then, subtract \( 318 \) from both sides: \[ 126 = 6.4x \] Now, solve for \( x \) by dividing both sides by \( 6.4 \): \[ x = \frac{126}{6.4} \] \[ x \approx 19.6875 \] Finally, substitute \( x \) back into one of the original equations to find \( y \). Using the equation for men: \[ y = 5(19.6875) + 444 \] \[ y \approx 542.4375 \] The solution is \( x \approx 19.6875 \) years after 1970 and \( y \approx 542.4375 \) thousand degrees.