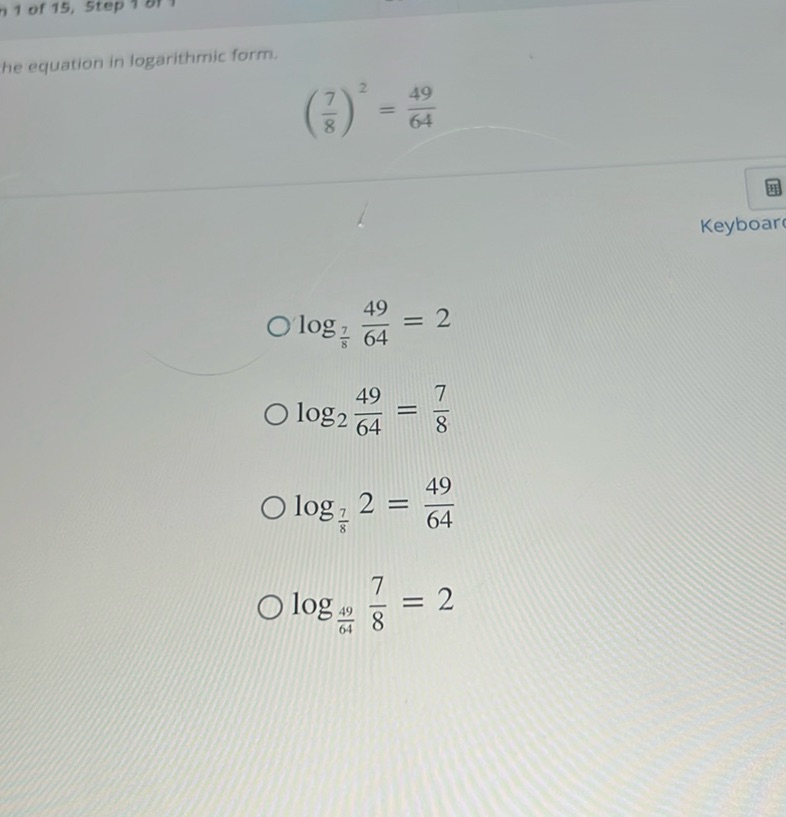
Question: The equation in logarithmic form. \[ \left(\frac{7}{8}\right)^2 = \frac{49}{64} \] Options:…

The equation in logarithmic form.

\[ \left(\frac{7}{8}\right)^2 = \frac{49}{64} \]

Options:

1. \(\log_{\frac{7}{8}} \frac{49}{64} = 2\)
2. \(\log_{2} \frac{49}{64} = \frac{7}{8}\)
3. \(\log_{\frac{7}{8}} 2 = \frac{49}{64}\)
4. \(\log_{\frac{49}{64}} \frac{7}{8} = 2\)

Solution

To express the equation in logarithmic form, start with the given equation: \[ \left(\frac{7}{8}\right)^2 = \frac{49}{64} \] Convert it into logarithmic form by using the fact that if \(a^b = c\), then \(\log_a c = b\). So, \(\left(\frac{7}{8}\right)^2 = \frac{49}{64}\) becomes: \[ \log_{\frac{7}{8}} \frac{49}{64} = 2 \] The correct option is: \[ \log_{\frac{7}{8}} \frac{49}{64} = 2 \]