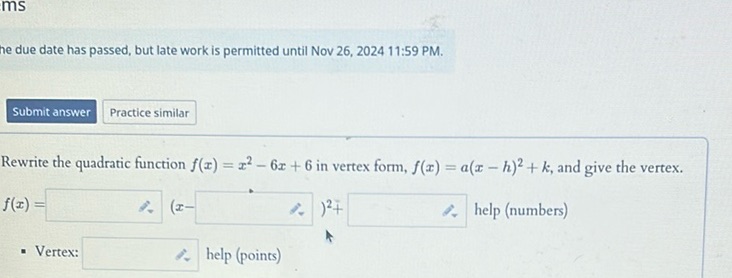
Question: The due date has passed, but late work is permitted until Nov 26, 2024 11:59 PM. Submit answer…

The due date has passed, but late work is permitted until Nov 26, 2024 11:59 PM.

Submit answer Practice similar

Rewrite the quadratic function \( f(x) = x^2 - 6x + 6 \) in vertex form, \( f(x) = a(x - h)^2 + k \), and give the vertex.

\( f(x) = \boxed{\phantom{xxxx}} (x - \boxed{\phantom{xxxx}})^2 + \boxed{\phantom{xxxx}} \) help (numbers)

Vertex: \( \boxed{\phantom{xxxx}} \) help (points)

Solution

To rewrite the quadratic function \( f(x) = x^2 - 6x + 6 \) in vertex form \( f(x) = a(x-h)^2 + k \), we need to complete the square. First, start with the original quadratic equation: \[ f(x) = x^2 - 6x + 6 \] Rewrite the equation by isolating the \(x\) terms: \[ f(x) = (x^2 - 6x) + 6 \] To complete the square, take half of the coefficient of \(x\), square it, and add and subtract it inside the parentheses. Half of \(-6\) is \(-3\), and squaring it gives 9. Add and subtract 9 inside the parentheses: \[ f(x) = (x^2 - 6x + 9 - 9) + 6 \] This can be rewritten as: \[ f(x) = ((x - 3)^2 - 9) + 6 \] Simplify inside the equation: \[ f(x) = (x - 3)^2 - 3 \] Now, the quadratic is in vertex form: \[ f(x) = 1(x - 3)^2 - 3 \] The vertex is \((h, k) = (3, -3)\).