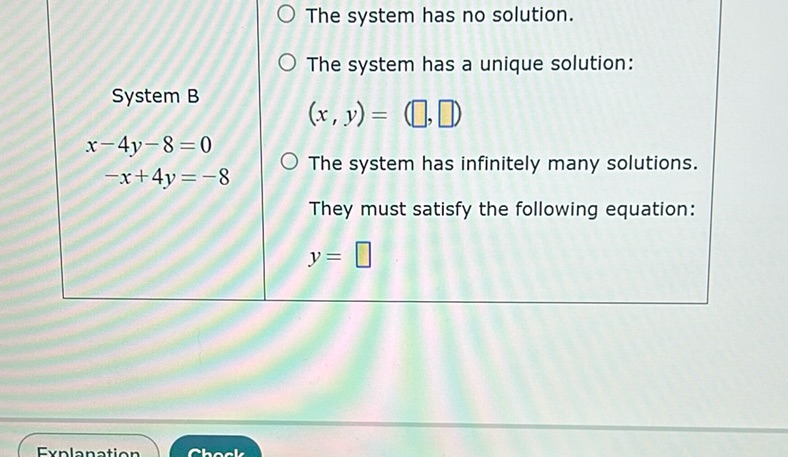
Question: System B \[ \begin{align*} x - 4y - 8 &= 0 \\ -x + 4y &= -8 \end{align*} \] - The system…

System B

\[ \begin{align*} x - 4y - 8 &= 0 \\ -x + 4y &= -8 \end{align*} \]

• The system has no solution.
• The system has a unique solution: \((x, y) = (\boxed{\phantom{0}}, \boxed{\phantom{0}})\)
• The system has infinitely many solutions. They must satisfy the following equation: \(y = \boxed{\phantom{0}}\)

Solution

The system of equations given is: \[ \begin{cases} x - 4y = 8 & \\ -x + 4y = -8 & \end{cases} \] First, add the two equations together to eliminate \(x\) and \(y\): \[ (x - 4y) + (-x + 4y) = 8 + (-8) \] This simplifies to: \[ 0 = 0 \] Since the result is a true statement, it means the system of equations has infinitely many solutions. The equations are dependent, so the system has infinitely many solutions. We can express \(y\) in terms of \(x\) using one of the original equations. Using the first equation: \[ x - 4y = 8 \] Solve for \(y\): \[ -4y = 8 - x \] \[ y = \frac{x - 8}{4} \] So, the system has infinitely many solutions, and they satisfy the equation: \[ y = \frac{x - 8}{4} \]