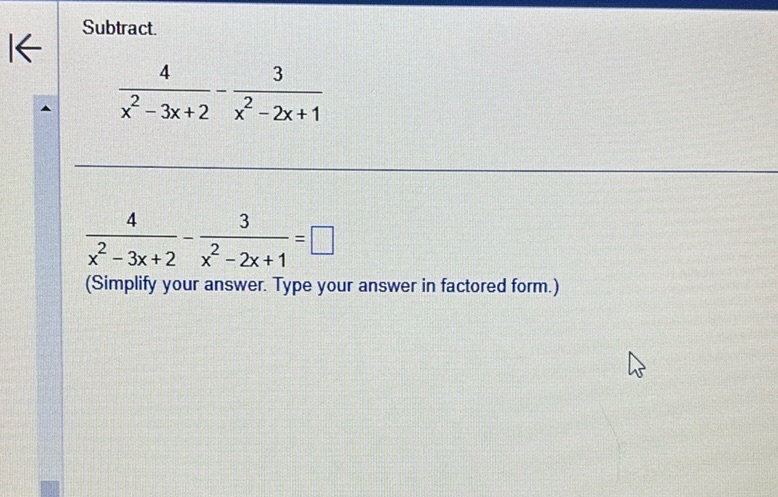
Question: Subtract. \frac{4}{x^2 - 3x + 2} - \frac{3}{x^2 - 2x + 1} \frac{4}{x^2 - 3x + 2} -…

Subtract. \frac{4}{x^2 - 3x + 2} - \frac{3}{x^2 - 2x + 1} \frac{4}{x^2 - 3x + 2} - \frac{3}{x^2 - 2x + 1} = \boxed{} (Simplify your answer. Type your answer in factored form.)

Solution

To solve the problem, we need to subtract the given rational expressions:

\[ \frac{4}{x^2 - 3x + 2} - \frac{3}{x^2 - 2x + 1} \]

First, factor the denominators.

For \(x^2 - 3x + 2\):

The factors are \((x - 1)(x - 2)\).

For \(x^2 - 2x + 1\):

This can be factored as \((x - 1)^2\).

Now, find a common denominator, which is \((x - 1)^2(x - 2)\).

Rewrite each fraction with the common denominator.

For \(\frac{4}{x^2 - 3x + 2}\):

\[ \frac{4}{(x - 1)(x - 2)} = \frac{4(x - 1)}{(x - 1)^2(x - 2)} \]

For \(\frac{3}{x^2 - 2x + 1}\):

\[ \frac{3}{(x - 1)^2} = \frac{3(x - 2)}{(x - 1)^2(x - 2)} \]

Now, subtract the two fractions:

\[ \frac{4(x - 1) - 3(x - 2)}{(x - 1)^2(x - 2)} \]

Simplify the numerator:

\[ 4(x - 1) = 4x - 4 \]

\[ 3(x - 2) = 3x - 6 \]

\[ 4x - 4 - (3x - 6) = 4x - 4 - 3x + 6 = x + 2 \]

So the expression becomes:

\[ \frac{x + 2}{(x - 1)^2(x - 2)} \]

This is the simplified form in factored terms.