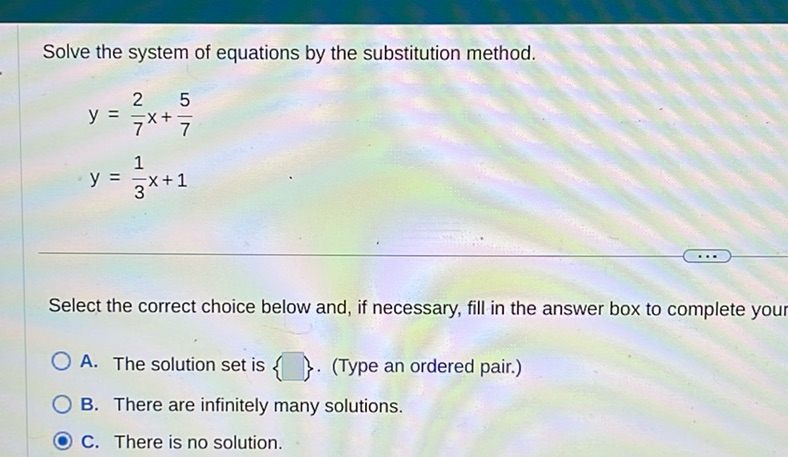
Question: Solve the system of equations by the substitution method. \[ y = \frac{2}{7}x + \frac{5}{7} \]…

Solve the system of equations by the substitution method.

\[ y = \frac{2}{7}x + \frac{5}{7} \]

\[ y = \frac{1}{3}x + 1 \]

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. The solution set is \(\boxed{\quad}\). (Type an ordered pair.)

B. There are infinitely many solutions.

C. There is no solution.

Solution

To solve the system of equations by the substitution method, we can set the two expressions for \( y \) equal to each other since both are equal to \( y \). \[ \frac{2}{7}x + \frac{5}{7} = \frac{1}{3}x + 1 \] Subtract \(\frac{1}{3}x\) from both sides: \[ \frac{2}{7}x - \frac{1}{3}x + \frac{5}{7} = 1 \] To eliminate the fractions, find a common denominator for \(\frac{2}{7}\) and \(\frac{1}{3}\), which is 21. Convert the fractions: \[ \frac{6}{21}x - \frac{7}{21}x + \frac{5}{7} = 1 \] Combine the \(x\) terms: \[ -\frac{1}{21}x + \frac{5}{7} = 1 \] Subtract \(\frac{5}{7}\) from both sides: \[ -\frac{1}{21}x = 1 - \frac{5}{7} \] Convert 1 to a fraction with a denominator of 7: \[ 1 = \frac{7}{7} \] Subtract the fractions: \[ 1 - \frac{5}{7} = \frac{7}{7} - \frac{5}{7} = \frac{2}{7} \] Now solve for \(x\): \[ -\frac{1}{21}x = \frac{2}{7} \] Multiply both sides by -21: \[ x = -21 \times \frac{2}{7} \] Calculate: \[ x = -3 \times 2 = -6 \] Substitute \( x = -6 \) back into one of the original equations to solve for \( y \). Using \( y = \frac{2}{7}x + \frac{5}{7} \): \[ y = \frac{2}{7}(-6) + \frac{5}{7} \] Calculate: \[ y = -\frac{12}{7} + \frac{5}{7} = -\frac{7}{7} = -1 \] Thus, the solution set is \((-6, -1)\). The correct choice is: A. The solution set is \((-6, -1)\).