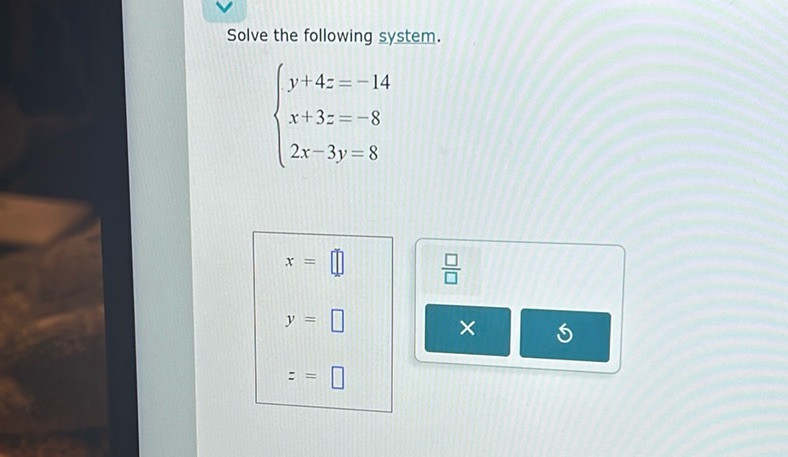
Question: Solve the following system: \[ \begin{cases} y + 4z = -14 \\ x + 3z = -8 \\ 2x - 3y = 8…

Solve the following system:

\[ \begin{cases} y + 4z = -14 \\ x + 3z = -8 \\ 2x - 3y = 8 \end{cases} \]

\( x = \boxed{\phantom{0}} \)

\( y = \boxed{\phantom{0}} \)

\( z = \boxed{\phantom{0}} \)

Solution

To solve the system of equations: \[ \begin{cases} y + 4z = -14 & \\ x + 3z = -8 & \\ 2x - 3y = 8 & \end{cases} \] First, solve for \( y \) in terms of \( z \) from the first equation: \[ y + 4z = -14 \] Subtract \( 4z \) from both sides: \[ y = -14 - 4z \] Next, solve for \( x \) in terms of \( z \) from the second equation: \[ x + 3z = -8 \] Subtract \( 3z \) from both sides: \[ x = -8 - 3z \] Substitute the expressions for \( x \) and \( y \) into the third equation: \[ 2x - 3y = 8 \] Substitute \( x = -8 - 3z \) and \( y = -14 - 4z \): \[ 2(-8 - 3z) - 3(-14 - 4z) = 8 \] Simplify the equation: \[ -16 - 6z + 42 + 12z = 8 \] Combine like terms: \[ 26 + 6z = 8 \] Subtract 26 from both sides: \[ 6z = 8 - 26 \] \[ 6z = -18 \] Divide by 6: \[ z = -3 \] Substitute \( z = -3 \) back into the expressions for \( x \) and \( y \): \[ x = -8 - 3(-3) \] \[ x = -8 + 9 \] \[ x = 1 \] \[ y = -14 - 4(-3) \] \[ y = -14 + 12 \] \[ y = -2 \] The solution to the system is: \( x = 1 \), \( y = -2 \), \( z = -3 \)