Question: Solve the following system. \[ \begin{cases} 2x - 3y + z = -7 \\ x - 2y = -6 \\ 3x + 4y = 2…

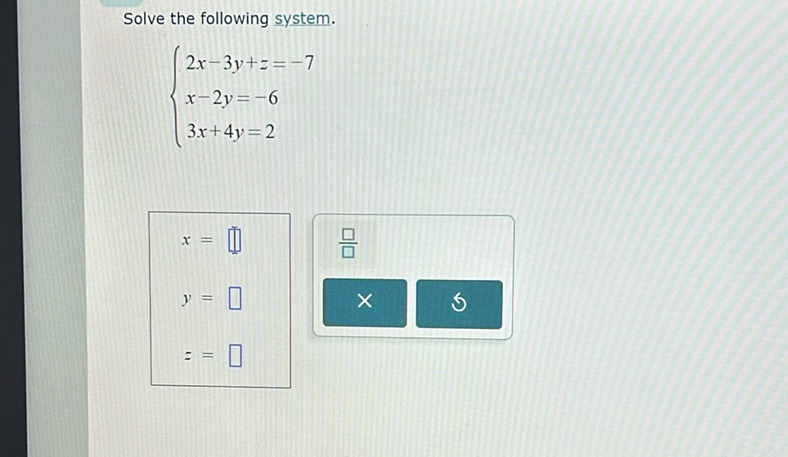
Solve the following system.

\[ \begin{cases} 2x - 3y + z = -7 \\ x - 2y = -6 \\ 3x + 4y = 2 \end{cases} \]

\( x = \) \(\square\)

\( y = \) \(\square\)

\( z = \) \(\square\)

Solution

We have the following system of equations to solve: \[ \begin{cases} 2x - 3y + z = -7 & \\ x - 2y = -6 & \\ 3x + 4y = 2 & \end{cases} \] First, solve the second equation for \(x\): \[ x = 2y - 6 \] Substitute \(x = 2y - 6\) into the first equation: \[ 2(2y - 6) - 3y + z = -7 \] Simplify: \[ 4y - 12 - 3y + z = -7 \] \[ y - 12 + z = -7 \] \[ y + z = 5 \quad \text{(Equation 4)} \] Now substitute \(x = 2y - 6\) into the third equation: \[ 3(2y - 6) + 4y = 2 \] Simplify: \[ 6y - 18 + 4y = 2 \] \[ 10y - 18 = 2 \] \[ 10y = 20 \] \[ y = 2 \] Substitute \(y = 2\) back into the equation for \(x\): \[ x = 2(2) - 6 \] \[ x = 4 - 6 \] \[ x = -2 \] Substitute \(y = 2\) into Equation 4: \[ 2 + z = 5 \] \[ z = 3 \] The solutions are: \[ x = -2, \quad y = 2, \quad z = 3 \]