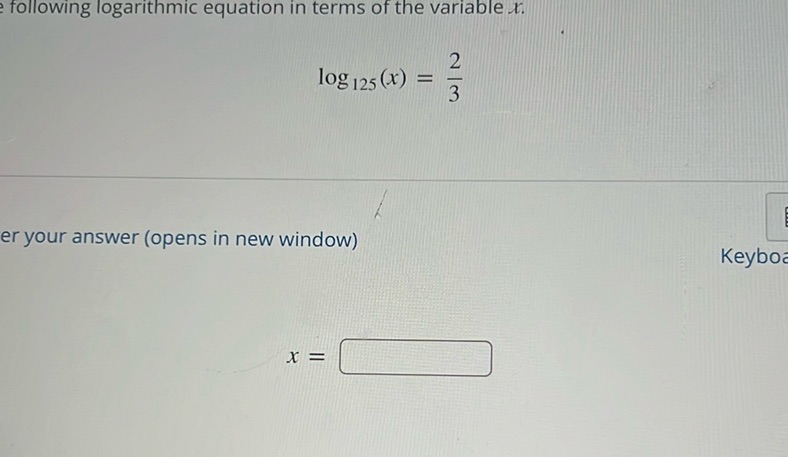
Question: Solve the following logarithmic equation in terms of the variable \( x \): \[ \log_{125}(x) =…

Solve the following logarithmic equation in terms of the variable \( x \):

\[ \log_{125}(x) = \frac{2}{3} \]

Enter your answer (opens in new window)

Keyboard

\( x = \boxed{\phantom{0}} \)

Solution

To solve the equation \(\log_{125}(x) = \frac{2}{3}\), we need to rewrite it in its exponential form. The logarithmic equation \(\log_{b}(a) = c\) can be rewritten as an exponential equation \(b^c = a\). In this case, \(b = 125\), \(a = x\), and \(c = \frac{2}{3}\). Rewriting the given equation: \[ 125^{\frac{2}{3}} = x \] Now, solve for \(x\): First, find \(125^{\frac{2}{3}}\). The exponent \(\frac{2}{3}\) means we take the cube root and then square the result. The cube root of 125 is 5, because \(5^3 = 125\). Next, square the result: \[ 5^2 = 25 \] Therefore, \[ x = 25 \] So, the value of \(x\) is 25.