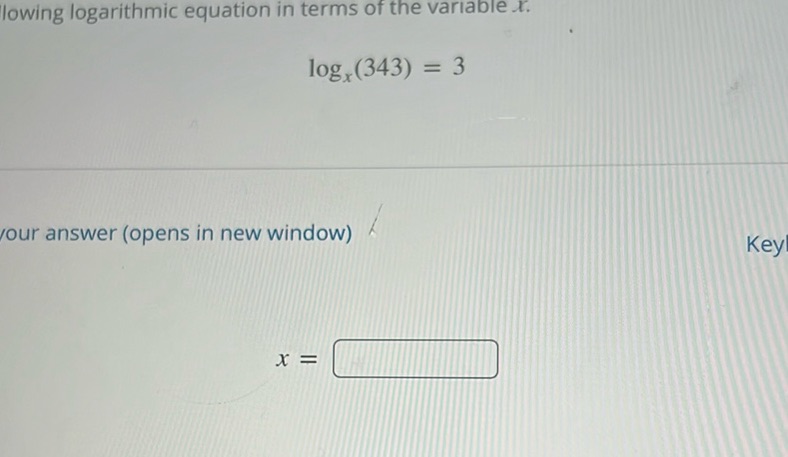
Question: Solve the following logarithmic equation in terms of the variable \( x \): \[ \log_x(343) = 3…

Solve the following logarithmic equation in terms of the variable \( x \):

\[ \log_x(343) = 3 \]

Your answer (opens in new window)

\( x = \boxed{\phantom{0}} \)

Solution

To solve the equation \(\log_x(343) = 3\), we need to convert the logarithmic equation to its exponential form. Start by understanding that \(\log_x(y) = z\) is equivalent to \(x^z = y\). Therefore, rewrite the equation \(\log_x(343) = 3\) as: \[ x^3 = 343 \] To find \(x\), take the cube root of both sides: \[ x = \sqrt[3]{343} \] Since 343 is \(7^3\), we find: \[ x = 7 \] So, the solution is \(x = 7\).