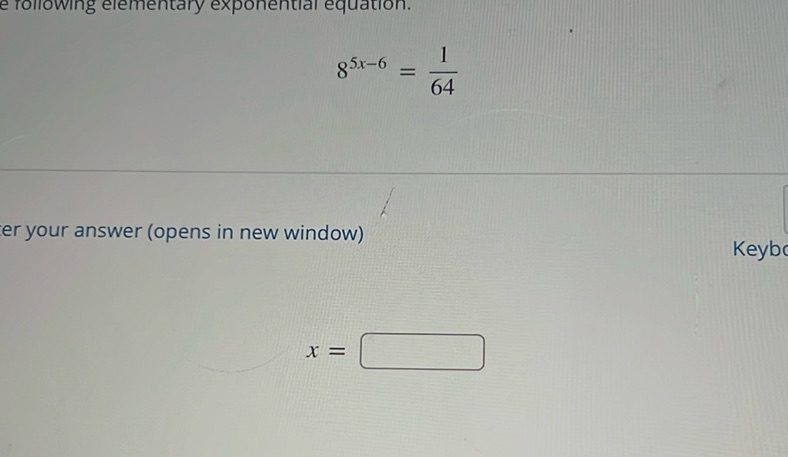
Question: Solve the following elementary exponential equation. \[ 8^{5x-6} = \frac{1}{64} \] Enter your…

Solve the following elementary exponential equation.

\[ 8^{5x-6} = \frac{1}{64} \]

Enter your answer (opens in new window)

\[ x = \boxed{\phantom{0}} \]

Solution

To solve the equation \( 8^{5x-6} = \frac{1}{64} \), we can rewrite both sides with the same base. First, rewrite \(\frac{1}{64}\) as a power of 8: \[ \frac{1}{64} = 8^{-2} \] Now, set the exponents equal because the bases are the same: \[ 5x - 6 = -2 \] Solve for \(x\): Add 6 to both sides: \[ 5x - 6 + 6 = -2 + 6 \] \[ 5x = 4 \] Divide both sides by 5: \[ x = \frac{4}{5} \] Therefore, \(x = \frac{4}{5}\).