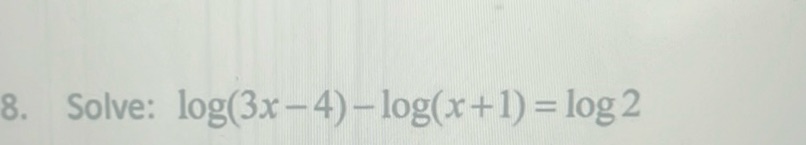
Question: Solve: \(\log(3x - 4) - \log(x + 1) = \log 2\)

Solution

Solve the equation: \[ \log(3x - 4) - \log(x + 1) = \log 2 \] Apply the logarithmic identity \(\log a - \log b = \log \frac{a}{b}\): \[ \log \left(\frac{3x - 4}{x + 1}\right) = \log 2 \] Since the logarithms are equal, set the arguments equal: \[ \frac{3x - 4}{x + 1} = 2 \] Clear the fraction by multiplying both sides by \(x + 1\): \[ 3x - 4 = 2(x + 1) \] Distribute on the right side: \[ 3x - 4 = 2x + 2 \] Subtract \(2x\) from both sides: \[ 3x - 2x = 2 + 4 \] Simplify: \[ x = 6 \] Check for any restrictions. The original expression \(\log(3x - 4)\) requires \(3x - 4 > 0\), so \(x > \frac{4}{3}\), and \(\log(x + 1)\) requires \(x + 1 > 0\), so \(x > -1\). The solution \(x = 6\) satisfies these conditions, so the solution is: \(x = 6\)