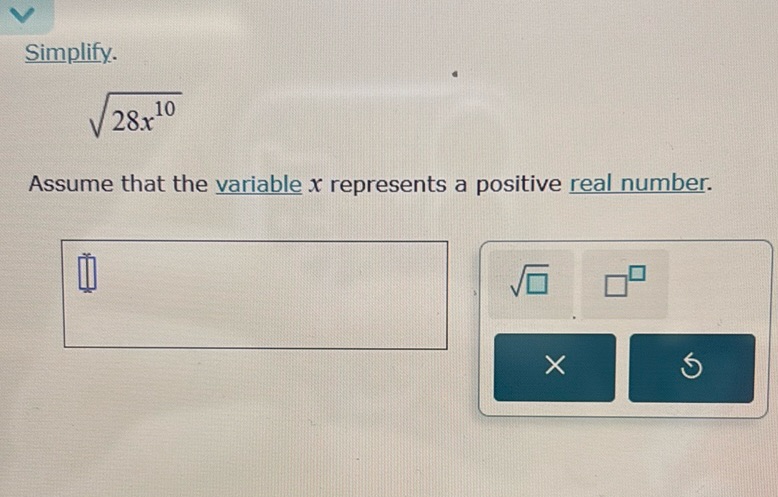
Question: Simplify. \(\sqrt{28x^{10}}\) Assume that the variable \(x\) represents a positive real…

Simplify.

\(\sqrt{28x^{10}}\)

Assume that the variable \(x\) represents a positive real number.

Solution

To simplify \(\sqrt{28x^{10}}\), follow these steps: First, separate the number and the variable inside the square root: \[ \sqrt{28x^{10}} = \sqrt{28} \times \sqrt{x^{10}} \] Next, simplify \(\sqrt{28}\): \(\sqrt{28} = \sqrt{4 \times 7} = \sqrt{4} \times \sqrt{7} = 2\sqrt{7}\) Now, simplify \(\sqrt{x^{10}}\): Since \(x^{10} = (x^5)^2\), we have \(\sqrt{x^{10}} = x^5\). Combine the simplified parts: \[ \sqrt{28x^{10}} = 2\sqrt{7} \times x^5 = 2x^5\sqrt{7} \] So, the simplified form is \(2x^5\sqrt{7}\).