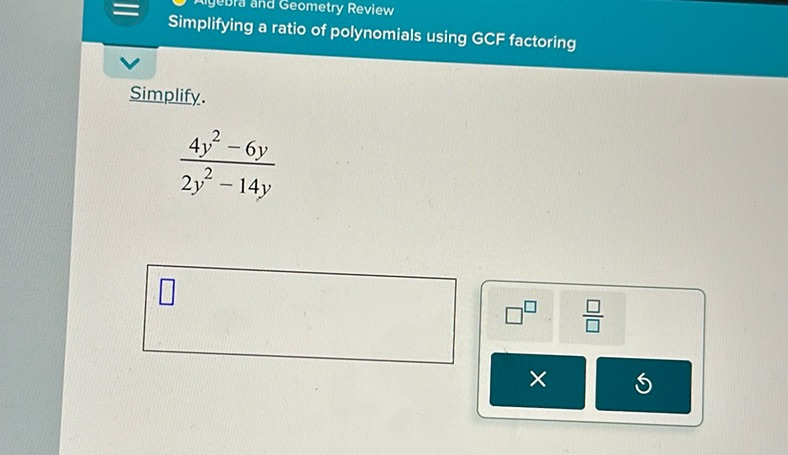
Question: Simplify. \frac{4y^2 - 6y}{2y^2 - 14y}

Solution

To simplify the given expression, we first factor out the greatest common factor (GCF) in both the numerator and the denominator. The expression is: \[ \frac{4y^2 - 6y}{2y^2 - 14y} \] Step 1: Factor out the GCF in the numerator. The GCF of \(4y^2\) and \(-6y\) is \(2y\). \[ 4y^2 - 6y = 2y(2y - 3) \] Step 2: Factor out the GCF in the denominator. The GCF of \(2y^2\) and \(-14y\) is \(2y\). \[ 2y^2 - 14y = 2y(y - 7) \] Step 3: Simplify the fraction by canceling out the common factor from the numerator and the denominator. \[ \frac{2y(2y - 3)}{2y(y - 7)} = \frac{2y - 3}{y - 7} \] The simplified form of the expression is: \[ \frac{2y - 3}{y - 7} \]