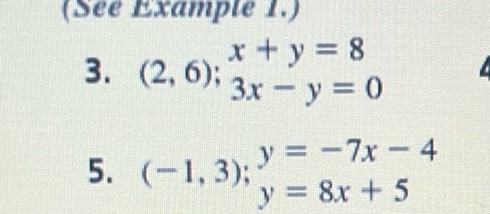
Question: (See Example 1.) 3. $(2, 6)$; $x + y = 8$ $3x - y = 0$ 5. $(-1, 3)$; $y = -7x - 4$ $y = 8x + 5$

(See Example 1.)

3. $(2, 6)$; $x + y = 8$ $3x - y = 0$

4. $(-1, 3)$; $y = -7x - 4$ $y = 8x + 5$

Solution

The photo shows two sets of systems of equations with points. Let’s solve each system to check if the given point satisfies the equations. ### Problem 3 Point: \((2, 6)\) Equations: \[ \begin{cases} x + y = 8 & \\ 3x - y = 0 & \end{cases} \] First, substitute \(x = 2\) and \(y = 6\) into the first equation: \(2 + 6 = 8\) This simplifies to: \(8 = 8\) Now, substitute \(x = 2\) and \(y = 6\) into the second equation: \(3(2) - 6 = 0\) This simplifies to: \(6 - 6 = 0\) \(0 = 0\) Both equations are satisfied by the point \((2, 6)\). ### Problem 5 Point: \((-1, 3)\) Equations: \[ \begin{cases} y = -7x - 4 & \\ y = 8x + 5 & \end{cases} \] First, substitute \(x = -1\) and \(y = 3\) into the first equation: \(3 = -7(-1) - 4\) This simplifies to: \(3 = 7 - 4\) \(3 = 3\) Now, substitute \(x = -1\) and \(y = 3\) into the second equation: \(3 = 8(-1) + 5\) This simplifies to: \(3 = -8 + 5\) \(3 = -3\) The point \((-1, 3)\) satisfies the first equation but not the second one.