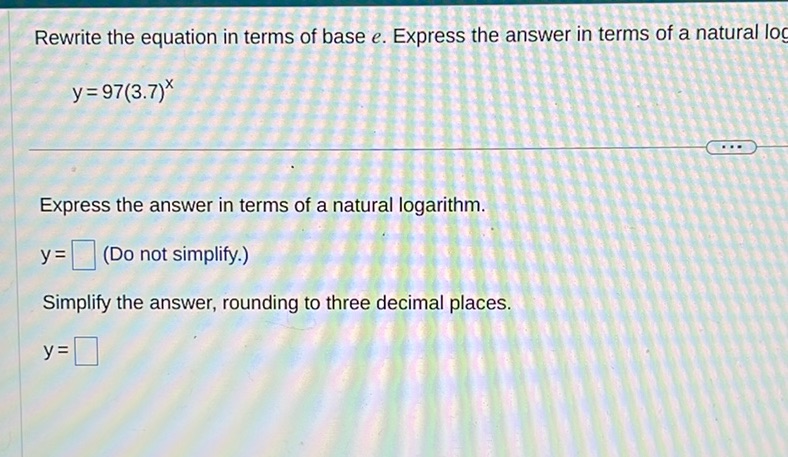
Question: Rewrite the equation in terms of base \( e \). Express the answer in terms of a natural…

Rewrite the equation in terms of base \( e \). Express the answer in terms of a natural logarithm.

\[ y = 97(3.7)^x \]

Express the answer in terms of a natural logarithm.

\[ y = \boxed{\phantom{0}} \text{ (Do not simplify.)} \]

Simplify the answer, rounding to three decimal places.

\[ y = \boxed{\phantom{0}} \]

Solution

To rewrite the equation in terms of base \( e \), we start with: \[ y = 97(3.7)^x \] We can express \( 3.7^x \) in terms of \( e \) by using the property that \( a^x = e^{x \ln a} \): \[ 3.7^x = e^{x \ln 3.7} \] Substitute this expression back into the equation for \( y \): \[ y = 97 \cdot e^{x \ln 3.7} \] So the expression in terms of a natural logarithm is: \[ y = 97 \cdot e^{x \ln 3.7} \] Now, simplify and round the answer to three decimal places. First, calculate \( \ln 3.7 \): \[ \ln 3.7 \approx 1.308 \] Substitute this back into the equation: \[ y = 97 \cdot e^{1.308x} \] This is the simplified expression rounded to three decimal places.