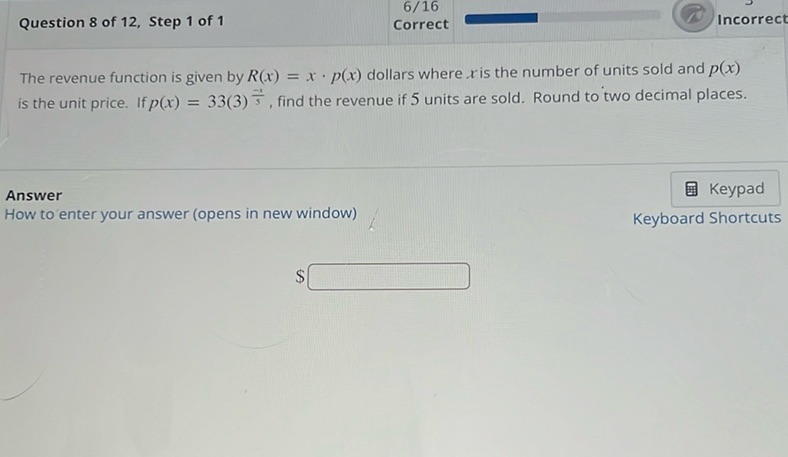
Question: Question 8 of 12, Step 1 of 1 The revenue function is given by \( R(x) = x \cdot p(x) \)…

Question 8 of 12, Step 1 of 1

The revenue function is given by \( R(x) = x \cdot p(x) \) dollars where \( x \) is the number of units sold and \( p(x) \) is the unit price. If \( p(x) = 33(3)^{\frac{1}{3}} \), find the revenue if 5 units are sold. Round to two decimal places.

Answer

How to enter your answer (opens in new window)

$

Solution

The problem gives the revenue function \( R(x) = x \cdot p(x) \), where \( x \) is the number of units sold and \( p(x) \) is the unit price. We are given \( p(x) = 33(3)^{\frac{x}{3}} \) and need to find the revenue when 5 units are sold. First, substitute \( x = 5 \) into the expression for \( p(x) \): \[ p(5) = 33(3)^{\frac{5}{3}} \] Calculate the exponent: \[ \frac{5}{3} \approx 1.67 \] Now calculate \( p(5) \): \[ p(5) = 33 \times 3^{1.67} \] Using a calculator, find \( 3^{1.67} \). Assume \( 3^{1.67} \approx 5.19 \) (rounded to two decimal places): \[ p(5) \approx 33 \times 5.19 = 171.27 \] Next, use the revenue function \( R(x) = x \cdot p(x) \) to find \( R(5) \): \[ R(5) = 5 \times 171.27 \] Calculate the revenue: \[ R(5) = 856.35 \] The revenue when 5 units are sold is approximately $856.35.