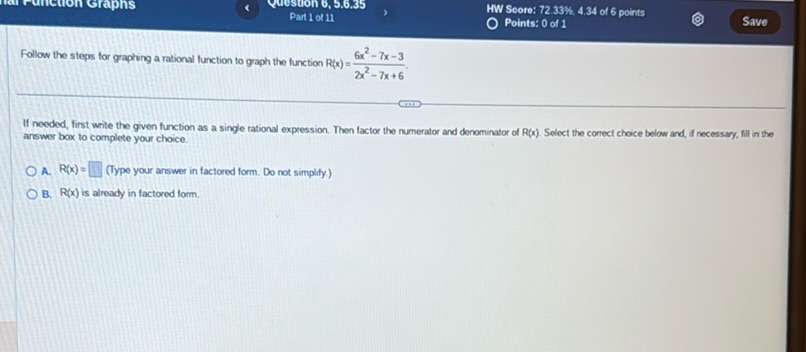
Question: Question 6, 5.8.35 Part 1 of 11 HW Score: 72.33%, 4.34 of 6 points **Points: 0 of…

Question 6, 5.8.35

Part 1 of 11

HW Score: 72.33%, 4.34 of 6 points

Points: 0 of 1

Save

Follow the steps for graphing a rational function to graph the function R(x) = \(\frac{6x^2 - 7x - 3}{2x^2 - 7x + 6}\)

If needed, first write the given function as a single rational expression. Then factor the numerator and denominator of R(x). Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. R(x) = \(\frac{\square}{\square}\) (Type your answer in factored form. Do not simplify.)

B. R(x) is already in factored form.

Solution

The problem requires factoring the given rational function \( R(x) = \frac{6x^2 - 7x - 3}{2x^2 - 7x + 6} \). We need to factor both the numerator and the denominator. Step 1: Factor the Numerator \(6x^2 - 7x - 3\) We look for two numbers whose product is \(6 \times (-3) = -18\) and whose sum is \(-7\). The numbers are \(-9\) and \(2\). Rewrite the middle term using these numbers: \[ 6x^2 - 9x + 2x - 3 \] Factor by grouping: \[ = 3x(2x - 3) + 1(2x - 3) \] \[ = (3x + 1)(2x - 3) \] Step 2: Factor the Denominator \(2x^2 - 7x + 6\) We look for two numbers whose product is \(2 \times 6 = 12\) and whose sum is \(-7\). The numbers are \(-3\) and \(-4\). Rewrite the middle term using these numbers: \[ 2x^2 - 3x - 4x + 6 \] Factor by grouping: \[ = x(2x - 3) - 2(2x - 3) \] \[ = (x - 2)(2x - 3) \] Conclusion The function in a factored form is: \[ R(x) = \frac{(3x + 1)(2x - 3)}{(x - 2)(2x - 3)} \] Choose: A. \(R(x) = \frac{(3x + 1)(2x - 3)}{(x - 2)(2x - 3)}\)