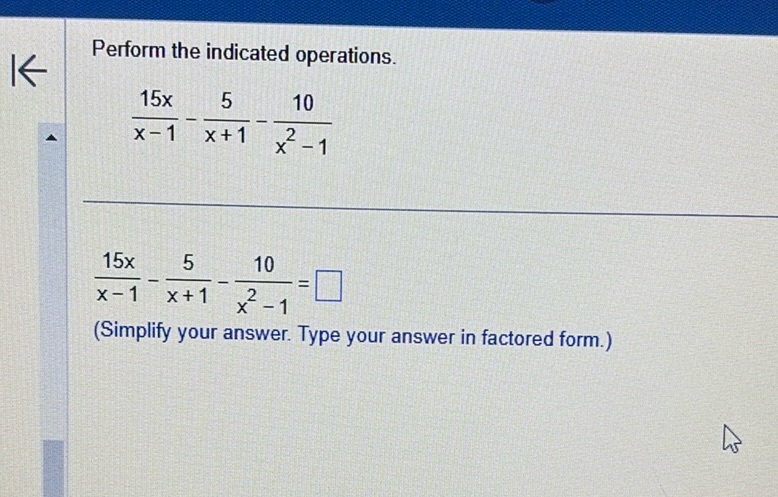
Question: Perform the indicated operations. \frac{15x}{x-1} - \frac{5}{x+1} - \frac{10}{x^2-1}…

Perform the indicated operations.

\frac{15x}{x-1} - \frac{5}{x+1} - \frac{10}{x^2-1}

\frac{15x}{x-1} - \frac{5}{x+1} - \frac{10}{x^2-1} = \square

(Simplify your answer. Type your answer in factored form.)

Solution

Find a common denominator.

\[ x^2 - 1 = (x - 1)(x + 1) \]

Rewrite each term with the common denominator.

\[ \frac{15x}{x - 1} = \frac{15x(x + 1)}{(x - 1)(x + 1)} \]

\[ \frac{5}{x + 1} = \frac{5(x - 1)}{(x - 1)(x + 1)} \]

\[ \frac{10}{x^2 - 1} = \frac{10}{(x - 1)(x + 1)} \]

Combine the fractions.

\[ \frac{15x(x + 1) - 5(x - 1) - 10}{(x - 1)(x + 1)} \]

Simplify the numerator.

\[ 15x^2 + 15x - 5x + 5 - 10 = 15x^2 + 10x - 5 \]

Factor the numerator.

\[ 5(3x^2 + 2x - 1) = 5(3x - 1)(x + 1) \]

Cancel \((x + 1)\).

\[ \frac{5(3x - 1)}{x - 1} \]

Answer:

\[ \frac{5(3x - 1)}{x - 1} \]