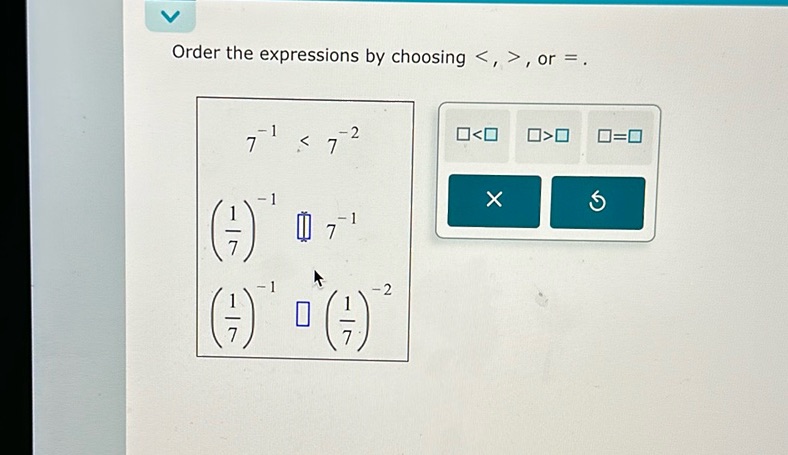
Question: Order the expressions by choosing <, >, or =. 7^{-1} < 7^{-2} (\frac{1}{7})^{-1} \square 7^{-1}…

Order the expressions by choosing <, >, or =. 7^{-1} < 7^{-2} (\frac{1}{7})^{-1} \square 7^{-1} (\frac{1}{7})^{-1} \square (\frac{1}{7})^{-2}

Solution

To compare the expressions, we need to simplify each one. First, let’s evaluate each expression: 1. \( 7^{-1} \) Using the rule \( a^{-n} = \frac{1}{a^n} \): \[ 7^{-1} = \frac{1}{7} \] 2. \( 7^{-2} \) \[ 7^{-2} = \frac{1}{7^2} = \frac{1}{49} \] 3. \(\left( \frac{1}{7} \right)^{-1}\) Using the same exponent rule, we have inversion: \[ \left( \frac{1}{7} \right)^{-1} = 7 \] 4. \(\left( \frac{1}{7} \right)^{-2}\) Using \( a^{-n} = \frac{1}{a^n} \): \[ \left( \frac{1}{7} \right)^{-2} = 7^2 = 49 \] Now, let’s compare: - \( \frac{1}{7} \) is greater than \( \frac{1}{49} \) because a larger denominator means a smaller fraction. - \( 7 \) is greater than \( \frac{1}{7} \). - \( 49 \) is greater than \( 7 \). So, the order from least to greatest is: \[ 7^{-2} < 7^{-1} < \left( \frac{1}{7} \right)^{-1} < \left( \frac{1}{7} \right)^{-2} \]