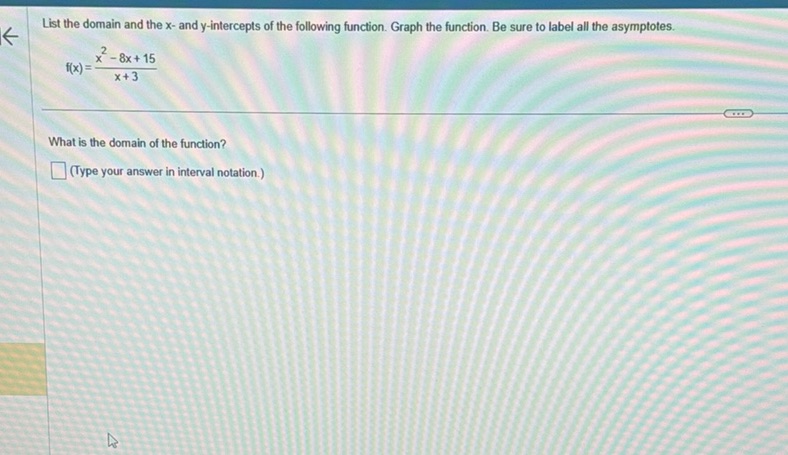
Question: List the domain and the x- and y-intercepts of the following function. Graph the function. Be sure…

List the domain and the x- and y-intercepts of the following function. Graph the function. Be sure to label all the asymptotes.

\[ f(x) = \frac{x^2 - 8x + 15}{x + 3} \]

What is the domain of the function?

(Type your answer in interval notation.)

Solution

Step 1: Determine the domain of the function. \[ x + 3 \neq 0 \] \[ x \neq -3 \] Therefore, the domain is: \[ (-\infty, -3) \cup (-3, \infty) \] Step 2: Find the x-intercepts. Set \( f(x) = 0 \): \[ \frac{x^2 - 8x + 15}{x + 3} = 0 \] This occurs when the numerator is zero: \[ x^2 - 8x + 15 = 0 \] Factor the quadratic: \[ (x - 3)(x - 5) = 0 \] \[ x = 3, \quad x = 5 \] So, the x-intercepts are at \( (3, 0) \) and \( (5, 0) \). Step 3: Find the y-intercept. Set \( x = 0 \): \[ f(0) = \frac{0^2 - 8(0) + 15}{0 + 3} = \frac{15}{3} = 5 \] So, the y-intercept is at \( (0, 5) \). Step 4: Determine the asymptotes. Vertical asymptote occurs where the denominator is zero: \[ x = -3 \] Since the degree of the numerator is greater than the denominator, perform polynomial division to find the oblique asymptote. Divide \( x^2 - 8x + 15 \) by \( x + 3 \): \[ x - 11 + \frac{48}{x + 3} \] Thus, the oblique asymptote is: \[ y = x - 11 \] Asymptotes: \[ \begin{cases} \text{Vertical asymptote: } x = -3 & \\ \text{Oblique asymptote: } y = x - 11 & \end{cases} \]