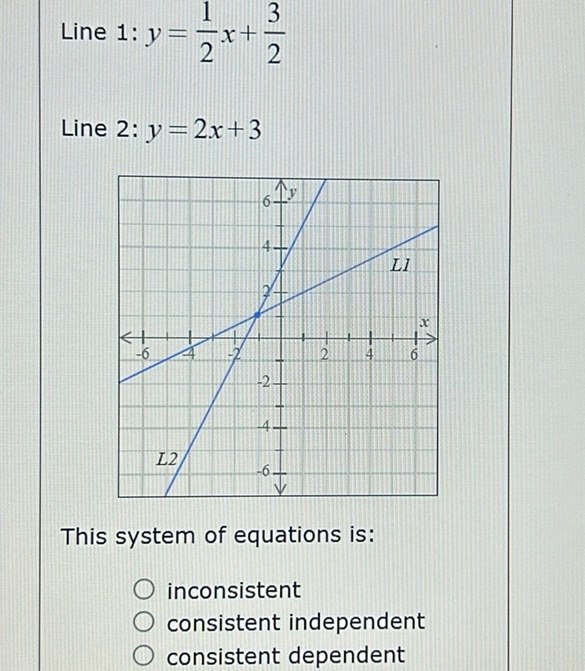
Question: Line 1: $y = \frac{1}{2}x + \frac{3}{2}$ Line 2: $y = 2x + 3$ [Graph of two lines intersecting…

Line 1: $y = \frac{1}{2}x + \frac{3}{2}$

Line 2: $y = 2x + 3$

[Graph of two lines intersecting at a point]

This system of equations is:

• inconsistent
• consistent independent
• consistent dependent

Solution

To determine the nature of the system of equations, we need to analyze the given equations for Line 1 and Line 2. Line 1: \[ y = \frac{1}{2}x + \frac{3}{2} \] Line 2: \[ y = 2x + 3 \] First, compare the slopes of the two lines. The slope of Line 1 is \( \frac{1}{2} \). The slope of Line 2 is \( 2 \). Since the slopes are not equal, the lines are not parallel and therefore intersect at exactly one point. This implies that the system of equations is consistent and independent.