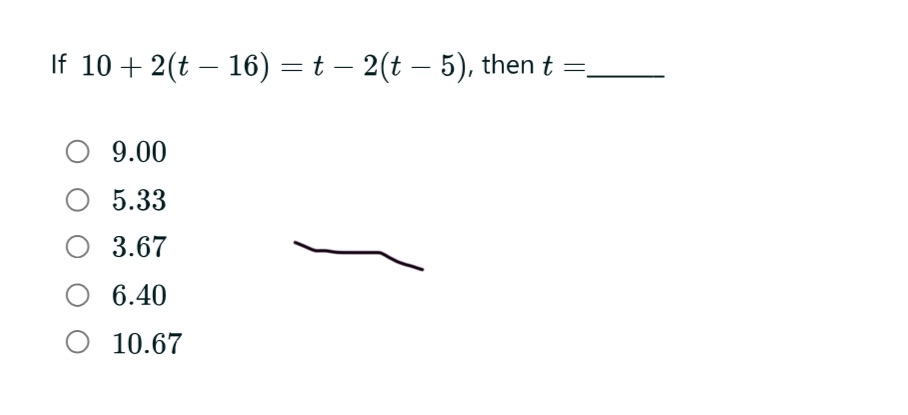
Question: If $10 + 2(t - 16) = t - 2(t - 5)$, then $t = \underline{\hspace{1cm}}$ $\circ \quad 9.00$…

If $10 + 2(t - 16) = t - 2(t - 5)$, then $t = \underline{\hspace{1cm}}$

$\circ \quad 9.00$

$\circ \quad 5.33$

$\circ \quad 3.67$

$\circ \quad 6.40$

$\circ \quad 10.67$

Solution

To solve the equation \(10 + 2(t - 16) = t - 2(t - 5)\), follow these steps: Start by distributing the terms: \(10 + 2t - 32 = t - 2t + 10\) Simplify both sides: \(2t - 22 = -t + 10\) Add \(t\) to both sides: \(2t + t - 22 = 10\) Combine like terms: \(3t - 22 = 10\) Add 22 to both sides: \(3t = 32\) Divide both sides by 3: \(t = \frac{32}{3}\) Calculate the final result: \(t = 10.67\) Therefore, the value of \(t\) is 10.67.