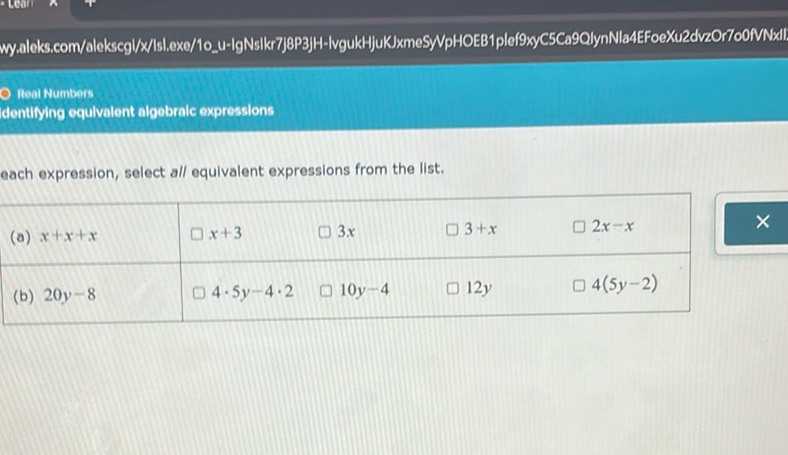
Question: Identifying equivalent algebraic expressions For each expression, select all equivalent…

Identifying equivalent algebraic expressions

For each expression, select all equivalent expressions from the list.

(a) \( x + x + x \)

• \( x + 3 \)
• \( 3x \)
• \( 3 + x \)
• \( 2x - x \)

(b) \( 20y - 8 \)

• \( 4 \cdot 5y - 4 \cdot 2 \)
• \( 10y - 4 \)
• \( 12y \)
• \( 4(5y - 2) \)

Solution

The task is to identify equivalent algebraic expressions. For (a) \(x + x + x\): First, combine like terms: \[ x + x + x = 3x \] Now, identify equivalent expressions from the list: - \(x + 3\) is not equivalent because it implies \(x + 3\). - \(3x\) is equivalent. - \(3 + x\) is not equivalent because it implies \(3 + x\). - \(2x - x\) is equivalent because: \[ 2x - x = x \] Thus, the equivalent expressions for \(x + x + x\) are \(3x\). For (b) \(20y - 8\): First, factor the expression: \[ 20y - 8 = 4(5y - 2) \] Now, identify equivalent expressions from the list: - \(4 \cdot 5y - 4 \cdot 2\) simplifies to: \[ 20y - 8 \] So this is equivalent. - \(10y - 4\) simplifies to: \[ 10y - 4 \] This is not equivalent. - \(12y\) is not equivalent because it doesn’t include \(-8\). - \(4(5y - 2)\) is equivalent because: \[ 4 \times (5y - 2) = 20y - 8 \] Thus, the equivalent expressions for \(20y - 8\) are \(4 \cdot 5y - 4 \cdot 2\) and \(4(5y - 2)\).