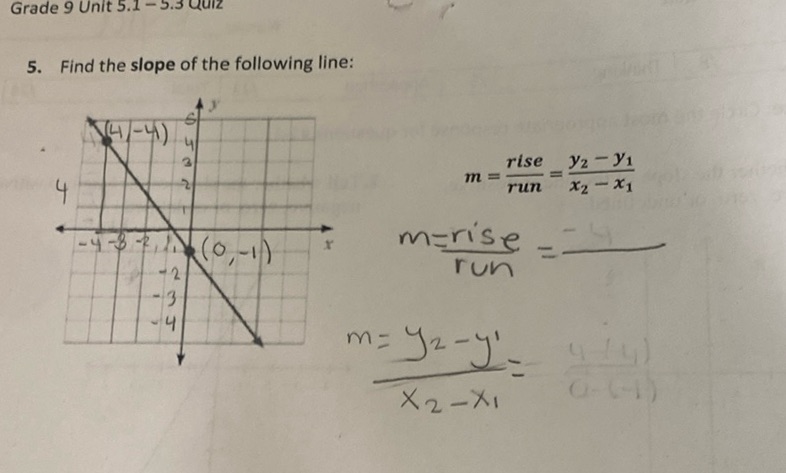
Question: Grade 9 Unit 5.1 - 5.3 Quiz 5. Find the slope of the following line: \[ \text{Graph:} \] \[…

Grade 9 Unit 5.1 - 5.3 Quiz

5. Find the slope of the following line:

\[ \text{Graph:} \]

\[ \begin{array}{c|c} x & y \\ \hline -4 & 4 \\ -3 & 3 \\ -2 & 2 \\ -1 & 1 \\ 0 & 0 \\ 1 & -1 \\ 2 & -2 \\ 3 & -3 \\ 4 & -4 \\ \end{array} \]

\[ m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1} \]

\[ m = \frac{\text{rise}}{\text{run}} = \frac{-5}{1} \]

\[ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - (-1)}{-4 - 0} \]

Solution

To find the slope of the line, we will use the formula for the slope \( m \), which is given by \[ m = \frac{y_2 - y_1}{x_2 - x_1} \] From the graph, two points on the line are \( (4, -4) \) and \( (0, -1) \). Assign the coordinates as follows: - \( (x_1, y_1) = (4, -4) \) - \( (x_2, y_2) = (0, -1) \) Substitute these values into the slope formula: \[ m = \frac{-1 - (-4)}{0 - 4} \] Simplify the numerator: \[ m = \frac{-1 + 4}{0 - 4} \] \[ m = \frac{3}{0 - 4} \] Simplify the denominator: \[ m = \frac{3}{-4} \] Therefore, the slope of the line is \[ m = -\frac{3}{4} \]