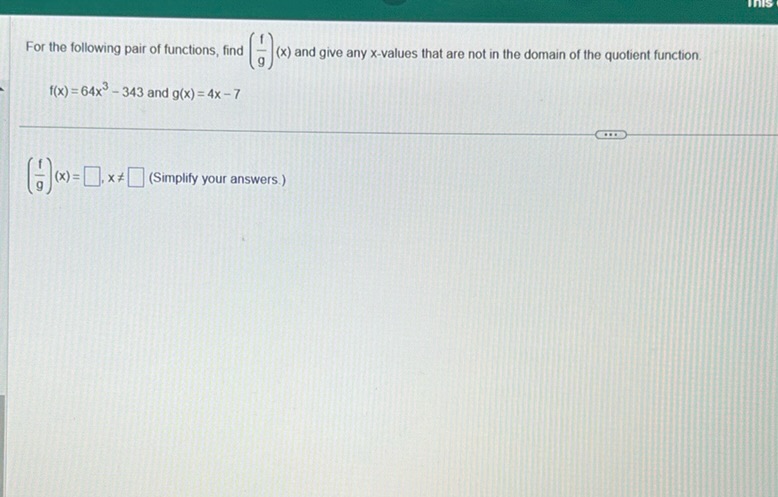
Question: For the following pair of functions, find \(\left( \frac{f}{g} \right)(x)\) and give any…

For the following pair of functions, find \(\left( \frac{f}{g} \right)(x)\) and give any \(x\)-values that are not in the domain of the quotient function.

\(f(x) = 64x^3 - 343\) and \(g(x) = 4x - 7\)

\(\left( \frac{f}{g} \right)(x) = \boxed{\phantom{xxxx}}\), \(x \neq \boxed{\phantom{xxxx}}\) (Simplify your answers.)

Solution

To solve for \( \left( \frac{f}{g} \right)(x) \) and determine any \( x \)-values that are not in the domain, follow these steps. First, find the quotient function: \[ \left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)} \] Substitute \( f(x) = 64x^3 - 343 \) and \( g(x) = 4x - 7 \): \[ \left( \frac{f}{g} \right)(x) = \frac{64x^3 - 343}{4x - 7} \] Next, identify any \( x \)-values not in the domain. The function \( g(x) \) must not be zero, so solve for \( x \) when \( g(x) = 4x - 7 = 0 \): \[ 4x - 7 = 0 \] \[ 4x = 7 \] \[ x = \frac{7}{4} \] Therefore, the value \( x = \frac{7}{4} \) is not in the domain of the quotient function. The final answer is: \[ \left( \frac{f}{g} \right)(x) = \frac{64x^3 - 343}{4x - 7}, \quad x \neq \frac{7}{4} \]