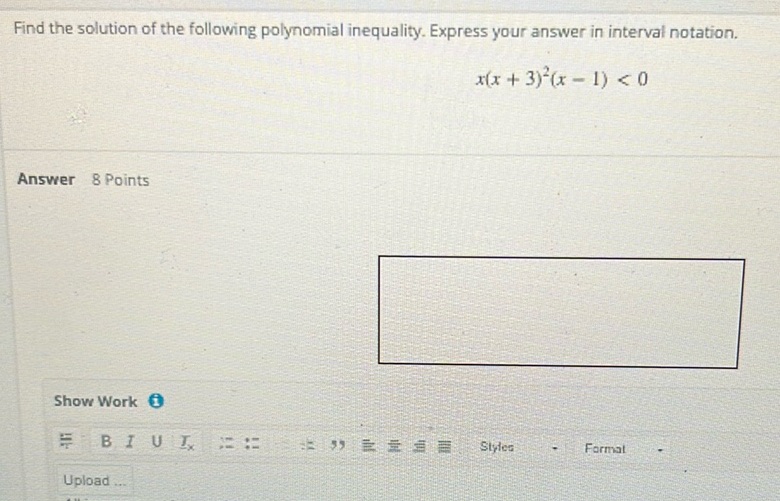
Question: Find the solution of the following polynomial inequality. Express your answer in interval notation…

Find the solution of the following polynomial inequality. Express your answer in interval notation.

\[ x(x + 3)^2(x - 1) < 0 \]

Answer: 8 Points

Solution

Step 1: Find the critical points by setting each factor equal to zero. \[ x = 0 \] \[ x + 3 = 0 \implies x = -3 \] \[ x - 1 = 0 \implies x = 1 \] Step 2: Determine the intervals based on the critical points. \[ (-\infty, -3),\ (-3, 0),\ (0, 1),\ (1, \infty) \] Step 3: Test the sign of the polynomial in each interval. For \(x < -3\), let \(x = -4\): \[ (-4)(-4 + 3)^2(-4 - 1) = (-4)(1)^2(-5) = 20 > 0 \] For \(-3 < x < 0\), let \(x = -1\): \[ (-1)(2)^2(-2) = 8 > 0 \] For \(0 < x < 1\), let \(x = 0.5\): \[ 0.5 \times (3.5)^2 \times (-0.5) = -3.0625 < 0 \] For \(x > 1\), let \(x = 2\): \[ 2 \times (5)^2 \times 1 = 50 > 0 \] Step 4: Determine where the polynomial is less than zero. The polynomial is negative in the interval \((0, 1)\). Thus, the solution in interval notation is: \[ (0, 1) \]