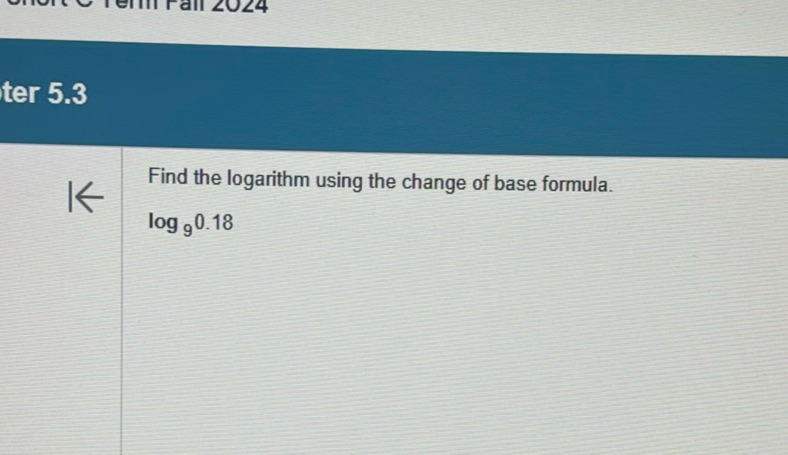
Question: Find the logarithm using the change of base formula. \(\log_{9} 0.18\)

Find the logarithm using the change of base formula.

\(\log_{9} 0.18\)

Solution

To find \(\log_5 0.18\) using the change of base formula, First, recall the change of base formula: \[ \log_b a = \frac{\log a}{\log b} \] Next, apply the formula to the given logarithm: \[ \log_5 0.18 = \frac{\log 0.18}{\log 5} \] Then, compute the logarithms using a calculator: \[ \log 0.18 \approx -0.7447 \] \[ \log 5 \approx 0.69897 \] Finally, calculate the value: \[ \log_5 0.18 = \frac{-0.7447}{0.69897} \approx -1.065 \]