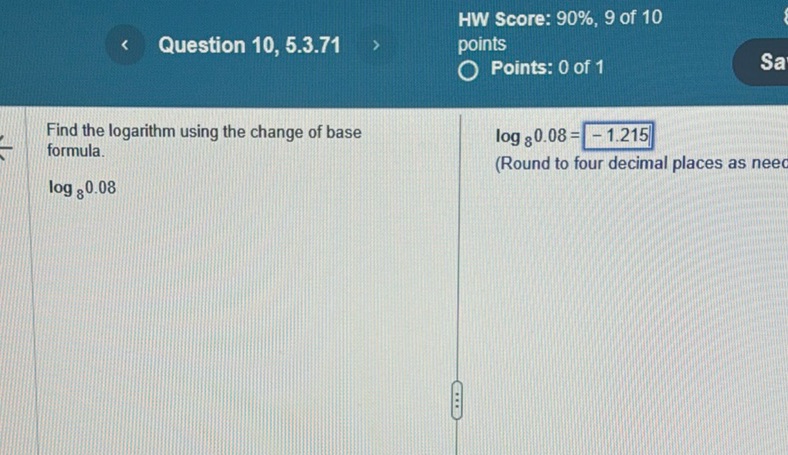
Question: Find the logarithm using the change of base formula. \(\log_{8} 0.08\) \(\log_{8} 0.08 =…

Find the logarithm using the change of base formula.

\(\log_{8} 0.08\)

\(\log_{8} 0.08 = -1.215\)

(Round to four decimal places as needed.)

Solution

To find \(\log_9 0.08\) using the change of base formula: Step 1 Apply the change of base formula: \[ \log_9 0.08 = \frac{\log 0.08}{\log 9} & \] Step 2 Calculate \(\log 0.08\): \[ \log 0.08 \approx -1.0969 & \] Step 3 Calculate \(\log 9\): \[ \log 9 \approx 0.9542 & \] Step 4 Divide the two values to find \(\log_9 0.08\): \[ \log_9 0.08 = \frac{-1.0969}{0.9542} \approx -1.1486 & \] After rounding to four decimal places, the final answer is: \[ \log_9 0.08 \approx -1.1486 & \]