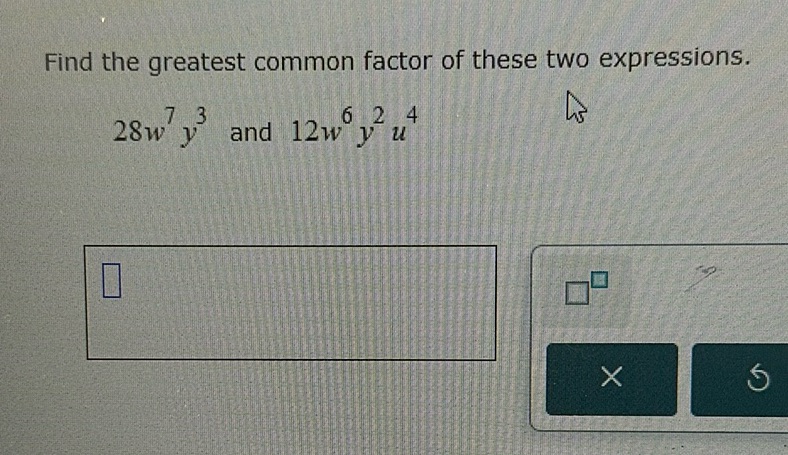
Question: Find the greatest common factor of these two expressions. $28w^7y^3$ and $12w^6y^2u^4$

Find the greatest common factor of these two expressions.

$28w^7y^3$ and $12w^6y^2u^4$

Solution

To find the greatest common factor (GCF) of the expressions \(28w^7y^3\) and \(12w^6y^2u^4\), we need to find the GCF of the coefficients, and each variable term separately. First, find the GCF of the coefficients 28 and 12. The factors of 28 are: 1, 2, 4, 7, 14, 28 The factors of 12 are: 1, 2, 3, 4, 6, 12 The greatest common factor of 28 and 12 is 4. Next, find the GCF of the variables: For \(w^7\) and \(w^6\), the GCF is \(w^6\), as we take the lower exponent. For \(y^3\) and \(y^2\), the GCF is \(y^2\), as we take the lower exponent. There is no \(u\) in the first expression, so it doesn’t contribute to the GCF. Combine these to find the overall GCF: The GCF is \[ 4w^6y^2 \] So, the greatest common factor of the expressions \(28w^7y^3\) and \(12w^6y^2u^4\) is \(4w^6y^2\).