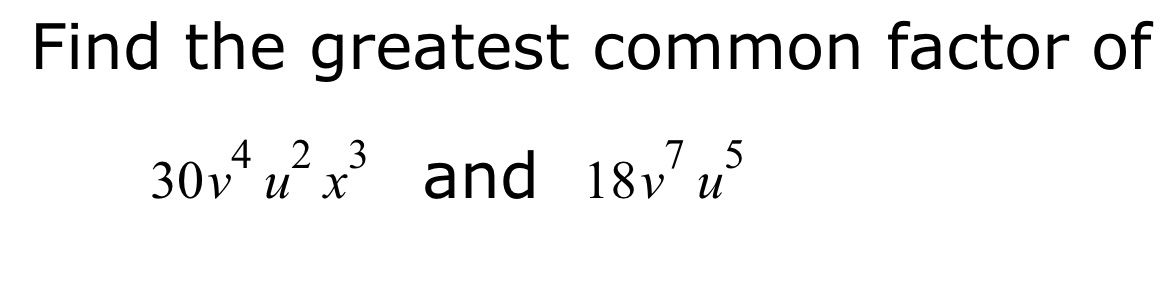
Question: Find the greatest common factor of $30v^4u^2x^3$ and $18v^7u^5$.

Find the greatest common factor of $30v^4u^2x^3$ and $18v^7u^5$.

Solution

To find the greatest common factor (GCF) of the expressions \(30v^4u^2x^3\) and \(18v^7u^5\), we should follow these steps: Identify the GCF of the coefficients: The coefficients are 30 and 18. The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30. The factors of 18 are 1, 2, 3, 6, 9, 18. The greatest common factor of 30 and 18 is 6. Identify the GCF for each variable: For \(v\), the terms are \(v^4\) and \(v^7\). The smallest power is \(v^4\). For \(u\), the terms are \(u^2\) and \(u^5\). The smallest power is \(u^2\). For \(x\), the first term is \(x^3\) and the other term does not have \(x\), so the common factor is \(x^0 = 1\). Combine these to find the overall GCF: \[ 6v^4u^2 \cdot 1 = 6v^4u^2 \] Thus, the greatest common factor is \(6v^4u^2\).