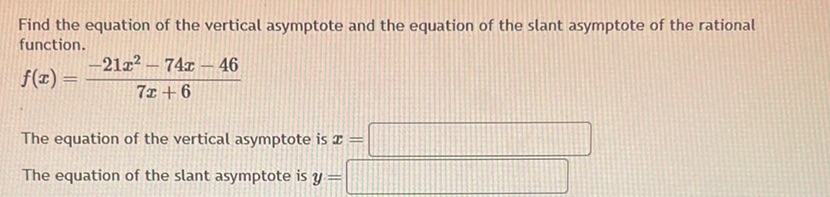
Question: Find the equation of the vertical asymptote and the equation of the slant asymptote of the rational…

Find the equation of the vertical asymptote and the equation of the slant asymptote of the rational function.

\[ f(x) = \frac{-21x^2 - 74x - 46}{7x + 6} \]

The equation of the vertical asymptote is \( x = \boxed{\phantom{xxxx}} \)

The equation of the slant asymptote is \( y = \boxed{\phantom{xxxx}} \)

Solution

To find the vertical asymptote, set the denominator equal to zero. \[ 7x + 6 = 0 \] Solve for \( x \): \[ x = -\frac{6}{7} \] The equation of the vertical asymptote is \( x = -\frac{6}{7} \). Next, to find the slant asymptote, perform polynomial long division of the numerator by the denominator. Divide \( -21x^2 - 74x - 46 \) by \( 7x + 6 \). First, divide \( -21x^2 \) by \( 7x \) to get \( -3x \). Multiply the divisor by \( -3x \): \[ -3x \times (7x + 6) = -21x^2 - 18x \] Subtract this from the original polynomial: \[ (-21x^2 - 74x) - (-21x^2 - 18x) = -56x \] Bring down \( -46 \): \[ -56x - 46 \] Next, divide \( -56x \) by \( 7x \) to get \( -8 \). Multiply the divisor by \( -8 \): \[ -8 \times (7x + 6) = -56x - 48 \] Subtract this from the current polynomial: \[ (-56x - 46) - (-56x - 48) = 2 \] The quotient is \( -3x - 8 \) with a remainder of \( 2 \). The equation of the slant asymptote is \( y = -3x - 8 \).