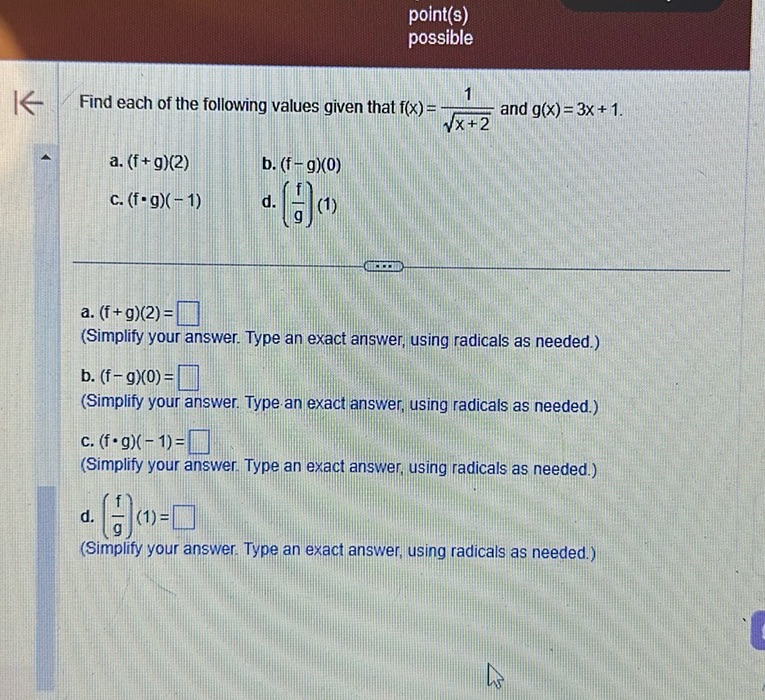
Question: Find each of the following values given that \( f(x) = \frac{1}{\sqrt{x + 2}} \) and \( g(x) =…

Find each of the following values given that \( f(x) = \frac{1}{\sqrt{x + 2}} \) and \( g(x) = 3x + 1 \).

a. \( (f + g)(2) \) b. \( (f - g)(0) \) c. \( (f \cdot g)(-1) \) d. \( \left( \frac{f}{g} \right)(1) \)

a. \( (f + g)(2) = \boxed{\phantom{0}} \) (Simplify your answer. Type an exact answer, using radicals as needed.)

b. \( (f - g)(0) = \boxed{\phantom{0}} \) (Simplify your answer. Type an exact answer, using radicals as needed.)

c. \( (f \cdot g)(-1) = \boxed{\phantom{0}} \) (Simplify your answer. Type an exact answer, using radicals as needed.)

d. \( \left( \frac{f}{g} \right)(1) = \boxed{\phantom{0}} \) (Simplify your answer. Type an exact answer, using radicals as needed.)

Solution

The given functions are \( f(x) = \frac{1}{\sqrt{x} + 2} \) and \( g(x) = 3x + 1 \). We need to find the following values: a. \( (f + g)(2) \) First, calculate \( f(2) \): \[ f(2) = \frac{1}{\sqrt{2} + 2} \] Next, calculate \( g(2) \): \[ g(2) = 3(2) + 1 = 6 + 1 = 7 \] Then, calculate \( (f + g)(2) \): \[ (f + g)(2) = f(2) + g(2) = \frac{1}{\sqrt{2} + 2} + 7 \] b. \( (f - g)(0) \) First, calculate \( f(0) \): \[ f(0) = \frac{1}{\sqrt{0} + 2} = \frac{1}{2} \] Next, calculate \( g(0) \): \[ g(0) = 3(0) + 1 = 1 \] Then, calculate \( (f - g)(0) \): \[ (f - g)(0) = f(0) - g(0) = \frac{1}{2} - 1 = \frac{1}{2} - \frac{2}{2} = -\frac{1}{2} \] c. \( (f \cdot g)(-1) \) First, calculate \( f(-1) \): \[ f(-1) = \frac{1}{\sqrt{-1} + 2} \] Since \( \sqrt{-1} \) is not a real number, \( f(-1) \) is undefined. d. \( \left(\frac{f}{g}\right)(1) \) First, calculate \( f(1) \): \[ f(1) = \frac{1}{\sqrt{1} + 2} = \frac{1}{1 + 2} = \frac{1}{3} \] Next, calculate \( g(1) \): \[ g(1) = 3(1) + 1 = 3 + 1 = 4 \] Then, calculate \( \left(\frac{f}{g}\right)(1) \): \[ \left(\frac{f}{g}\right)(1) = \frac{f(1)}{g(1)} = \frac{\frac{1}{3}}{4} = \frac{1}{12} \]