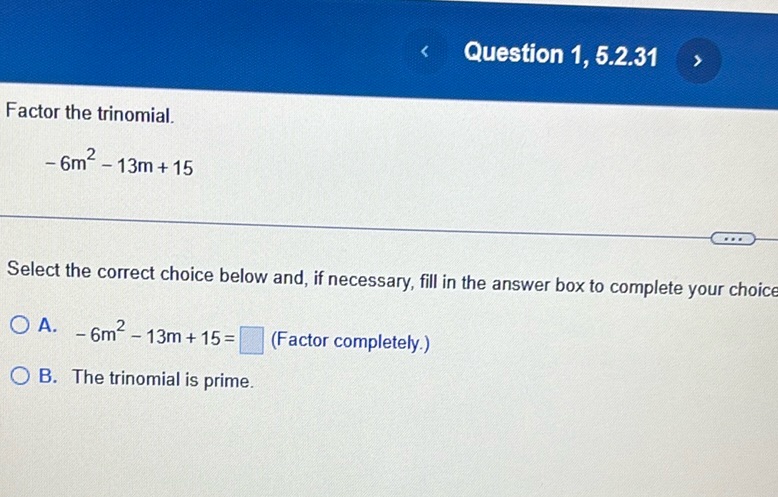
Question: Factor the trinomial. $-6m^2 - 13m + 15$ Select the correct choice below and, if necessary, fill…

Factor the trinomial.

$-6m^2 - 13m + 15$

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. $-6m^2 - 13m + 15 = \boxed{\phantom{0}}$ (Factor completely.)

B. The trinomial is prime.

Solution

The problem is to factor the trinomial: \[ -6m^2 - 13m + 15 \] First, identify a common factor in all terms. In this case, there isn’t a common factor other than 1. Next, try to factor by grouping or by using the quadratic trinomial method. We are looking for two numbers that multiply to \(a \cdot c = -6 \cdot 15 = -90\) and add to \(b = -13\). The two numbers that work are -18 and 5, since \(-18 \times 5 = -90\) and \(-18 + 5 = -13\). Rewrite the middle term using -18 and 5: \[ -6m^2 - 18m + 5m + 15 \] Group the terms: \[ (-6m^2 - 18m) + (5m + 15) \] Factor out the greatest common factor from each group: \[ -6m(m + 3) + 5(m + 3) \] Since \(m + 3\) is common, factor it out: \[ (m + 3)(-6m + 5) \] So, the trinomial factors to: \[ (m + 3)(-6m + 5) \] The answer is choice A.