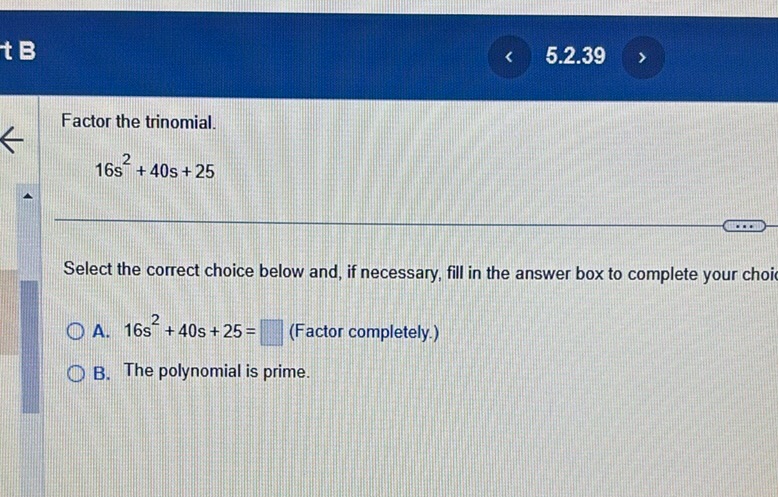
Question: Factor the trinomial. $$16s^2 + 40s + 25$$ Select the correct choice below and, if necessary,…

Factor the trinomial.

$$16s^2 + 40s + 25$$

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. $16s^2 + 40s + 25 = \boxed{\phantom{0}}$ (Factor completely.)

B. The polynomial is prime.

Solution

To factor the trinomial \(16s^2 + 40s + 25\), follow these steps: First, identify the form of the quadratic trinomial, which is \(ax^2 + bx + c\). Here, \(a = 16\), \(b = 40\), and \(c = 25\). Check if the trinomial can be factored as a perfect square trinomial. A trinomial \(ax^2 + bx + c\) is a perfect square if: \[ b^2 = 4ac \] Calculate \(b^2\): \[ b^2 = 40^2 = 1600 \] Calculate \(4ac\): \[ 4ac = 4 \times 16 \times 25 = 1600 \] Since \(b^2 = 4ac\), the trinomial is a perfect square. Factor the trinomial as a perfect square: The standard form of a perfect square trinomial is \((mx + n)^2\) where: \[ m^2 = a \quad \text{and} \quad n^2 = c \] Here, \(m = \sqrt{16} = 4\) and \(n = \sqrt{25} = 5\). Thus, the trinomial can be factored as: \[ (4s + 5)^2 \] The complete factorization of the trinomial \(16s^2 + 40s + 25\) is \( (4s + 5)^2 \). Therefore, the correct choice is: A. \(16s^2 + 40s + 25 = (4s + 5)^2\) (Factor completely.)