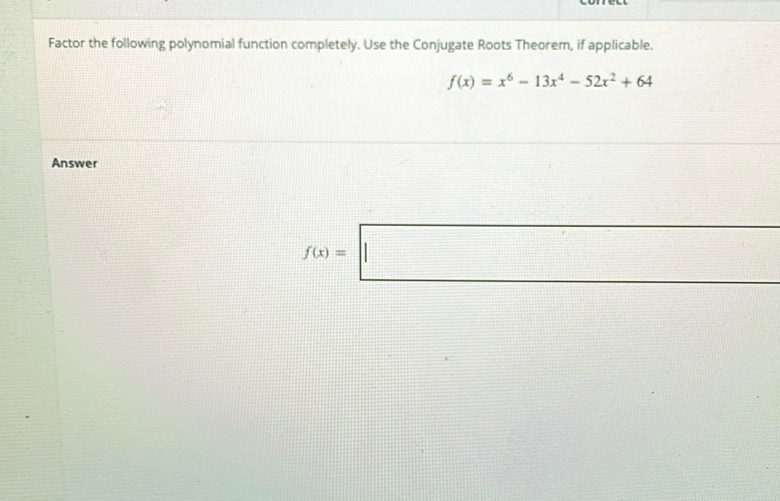
Question: Factor the following polynomial function completely. Use the Conjugate Roots Theorem, if…

Factor the following polynomial function completely. Use the Conjugate Roots Theorem, if applicable.

\[ f(x) = x^6 - 13x^4 - 52x^2 + 64 \]

Answer

\[ f(x) = \]

Solution

Let’s solve the problem step by step. Let \( y = x^2 \) & Substitute \( y \) into the polynomial function: \[ f(x) = y^3 - 13y^2 - 52y + 64 & \] Find the roots of the cubic equation \( y^3 - 13y^2 - 52y + 64 = 0 \). Testing \( y = 1 \): \[ 1^3 - 13(1)^2 - 52(1) + 64 = 0 & \] So, \( y = 1 \) is a root. Factor the cubic polynomial: \[ f(x) = (y - 1)(y^2 - 12y - 64) & \] Factor the quadratic \( y^2 - 12y - 64 \): \[ y^2 - 12y - 64 = (y - 16)(y + 4) & \] Substitute back \( y = x^2 \): \[ (x^2 - 1)(x^2 - 16)(x^2 + 4) & \] Factor each quadratic: \[ (x - 1)(x + 1)(x - 4)(x + 4)(x - 2i)(x + 2i) & \] So, the completely factored form of the polynomial is: \[ f(x) = (x - 1)(x + 1)(x - 4)(x + 4)(x - 2i)(x + 2i) & \]