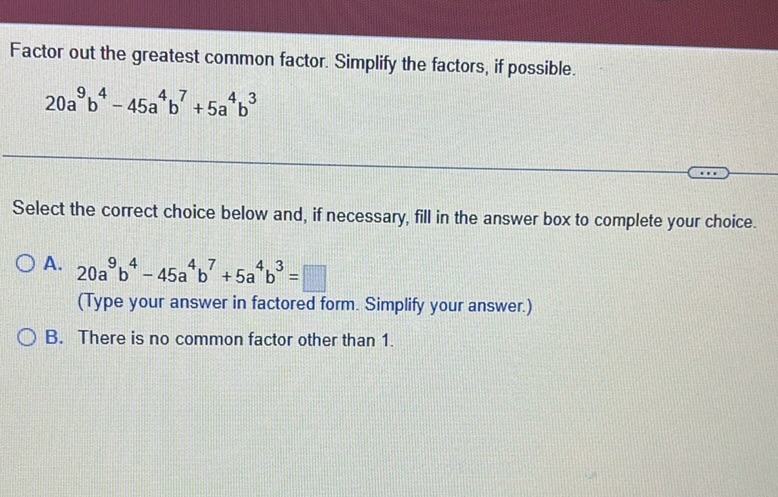
Question: Factor out the greatest common factor. Simplify the factors, if possible. \[ 20a^9 b^4 - 45a^4…

Factor out the greatest common factor. Simplify the factors, if possible.

\[ 20a^9 b^4 - 45a^4 b^7 + 5a^4 b^3 \]

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. \( 20a^9 b^4 - 45a^4 b^7 + 5a^4 b^3 = \) (Type your answer in factored form. Simplify your answer.)

B. There is no common factor other than 1.

Solution

To factor out the greatest common factor, let’s first identify the greatest common factor from the terms in the expression: \[ 20a^9b^4 - 45a^7b + 5a^4b^3 \] 1. Look at the numerical coefficients: 20, 45, and 5. The greatest common factor is 5. 2. Look at the variable \(a\): the smallest power of \(a\) is \(a^4\). 3. Look at the variable \(b\): the smallest power of \(b\) is \(b\). The greatest common factor is \(5a^4b\). Now, factor \(5a^4b\) out of the expression: \[ \begin{align*} 20a^9b^4 - 45a^7b + 5a^4b^3 &= 5a^4b(4a^5b^3) - 5a^4b(9a^3) + 5a^4b(b^2) \\ &= 5a^4b(4a^5b^3 - 9a^3 + b^2) \end{align*} \] The factored expression is: \[ 5a^4b(4a^5b^3 - 9a^3 + b^2) \]