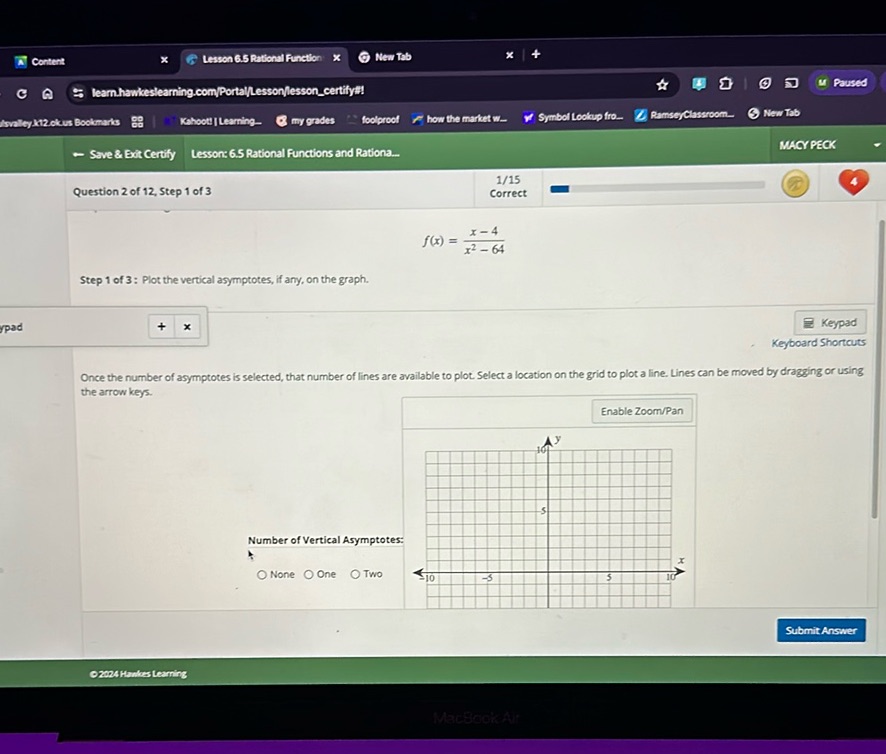
Question: f(x) = \frac{x - 4}{x^2 - 64}

Solution

To find the vertical asymptotes of the function \[ f(x) = \frac{x - 4}{x^2 - 64} \] we need to determine where the denominator equals zero (since asymptotes occur where the function is undefined). First, set the denominator equal to zero: \[ x^2 - 64 = 0 \] Next, factor the equation: \[ (x - 8)(x + 8) = 0 \] Now, solve for \(x\): \[ \begin{cases} x - 8 = 0 & \\ x + 8 = 0 & \end{cases} \] This gives us: \[ \begin{cases} x = 8 & \\ x = -8 & \end{cases} \] Therefore, the vertical asymptotes are at \(x = 8\) and \(x = -8\).