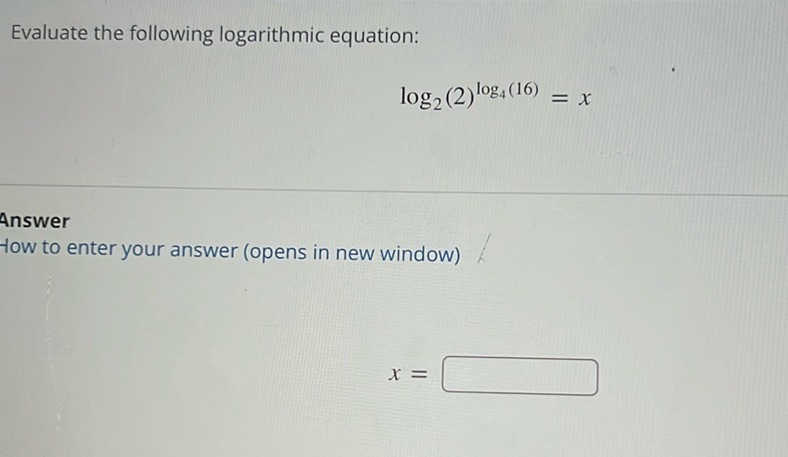
Question: Evaluate the following logarithmic equation: \[ \log_2(2)^{\log_4(16)} = x \] Answer How to…

Evaluate the following logarithmic equation:

\[ \log_2(2)^{\log_4(16)} = x \]

Answer

How to enter your answer (opens in new window)

\[ x = \boxed{\quad} \]

Solution

To solve the logarithmic equation: \[ \log_2(2)^{\log_4(16)} = x \] First, evaluate \(\log_2(2)\). \[ \log_2(2) = 1 \] Now, evaluate \(\log_4(16)\). Since \(16 = 4^2\), we have: \[ \log_4(16) = \log_4(4^2) = 2 \cdot \log_4(4) = 2 \cdot 1 = 2 \] Now substitute back into the expression: \[ 1^{\log_4(16)} = 1^2 = 1 \] Therefore, \(x = 1\). So, the answer is: \[ x = 1 \]