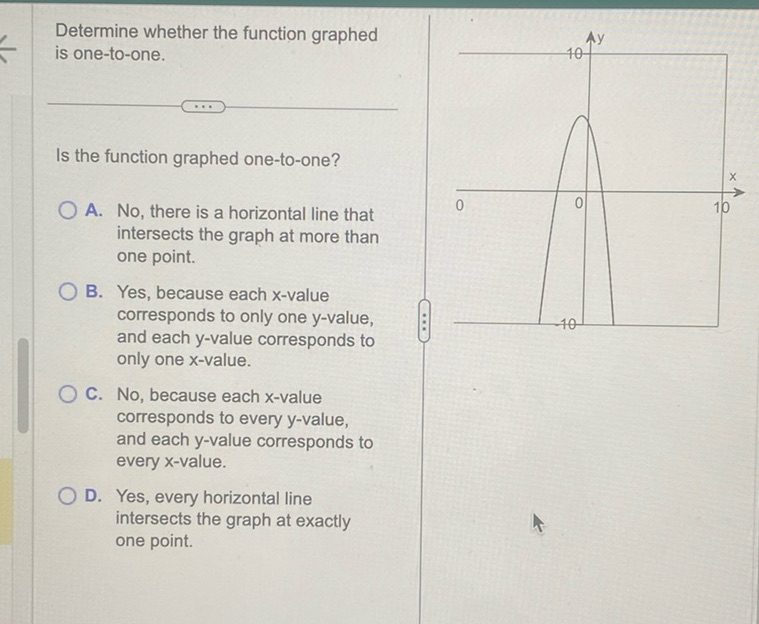
Question: Determine whether the function graphed is one-to-one. Is the function graphed one-to-one? A. No,…

Determine whether the function graphed is one-to-one.

Is the function graphed one-to-one?

A. No, there is a horizontal line that intersects the graph at more than one point.

B. Yes, because each x-value corresponds to only one y-value, and each y-value corresponds to only one x-value.

C. No, because each x-value corresponds to every y-value, and each y-value corresponds to every x-value.

D. Yes, every horizontal line intersects the graph at exactly one point.

[Graph of a function with a peak at the origin and symmetric about the y-axis, showing that it is not one-to-one.]

Solution

The problem is asking whether the function graphed is one-to-one. To determine if a function is one-to-one, we need to use the horizontal line test. A function is one-to-one if and only if no horizontal line intersects its graph at more than one point. Looking at the graph: - The function appears to be a parabola opening downwards. - A horizontal line drawn through the graph would intersect it at more than one point in the upper region. This means that the function is not one-to-one. Therefore, the correct answer is: A. No, there is a horizontal line that intersects the graph at more than one point.