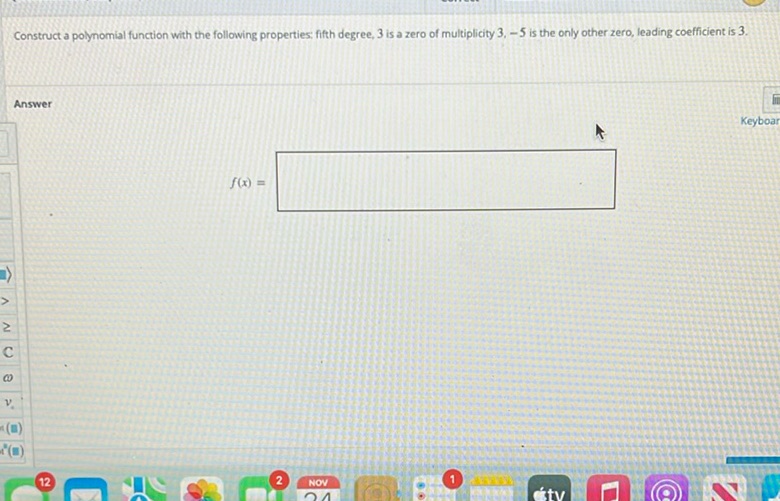
Question: Construct a polynomial function with the following properties: fifth degree, 3 is a zero of…

Construct a polynomial function with the following properties: fifth degree, 3 is a zero of multiplicity 3, -5 is the only other zero, leading coefficient is 3.

Answer

\[ f(x) = \]

Solution

To construct the polynomial function with the given properties: Step 1: Identify the factors based on the zeros and their multiplicities. Since 3 is a zero of multiplicity 3 and -5 is the only other zero, the factors are \((x - 3)^3\) and \((x + 5)\). \[ f(x) = (x - 3)^3 (x + 5) \] Step 2: Apply the leading coefficient of 3 to the polynomial. \[ f(x) = 3(x - 3)^3 (x + 5) \] The polynomial function is: \[ f(x) = 3(x - 3)^3 (x + 5) \]