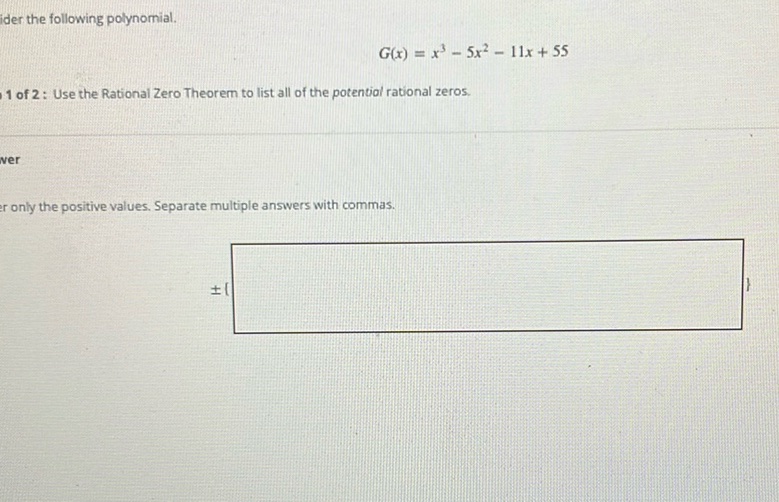
Question: Consider the following polynomial. \[ G(x) = x^3 - 5x^2 - 11x + 55 \] Part 1 of 2: Use the…

Consider the following polynomial.

\[ G(x) = x^3 - 5x^2 - 11x + 55 \]

Part 1 of 2: Use the Rational Zero Theorem to list all of the potential rational zeros.

Answer only the positive values. Separate multiple answers with commas.

\[ \pm \{ \} \]

Solution

Identify the constant term and leading coefficient of the polynomial. \[ \text{Constant term} = 55 & \] \[ \text{Leading coefficient} = 1 & \] List the factors of the constant term. \[ \text{Factors of } 55 = \pm1, \pm5, \pm11, \pm55 & \] List the factors of the leading coefficient. \[ \text{Factors of } 1 = \pm1 & \] Apply the Rational Zero Theorem. \[ \text{Possible rational zeros} = \frac{\text{factors of constant term}}{\text{factors of leading coefficient}} = \pm1, \pm5, \pm11, \pm55 & \] Only enter the positive values separated by commas. Answer: 1,5,11,55