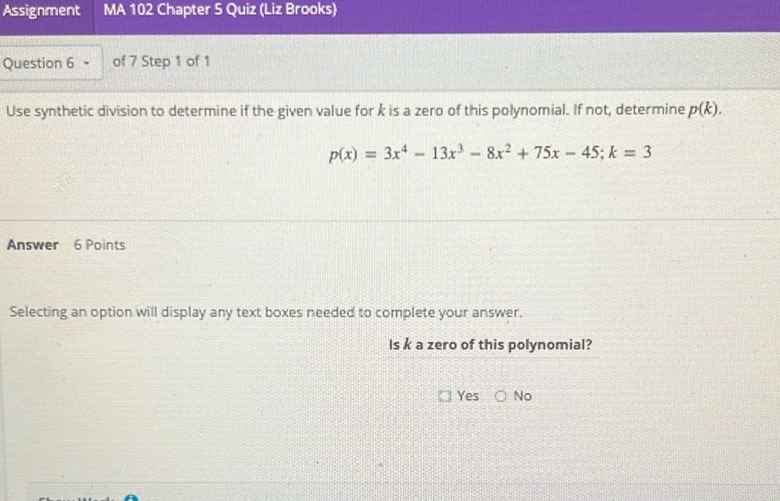
Question: Assignment MA 102 Chapter 5 Quiz (Liz Brooks) Question 6 - of 7 Step 1 of 1 Use synthetic…

Assignment MA 102 Chapter 5 Quiz (Liz Brooks)

Question 6 - of 7 Step 1 of 1

Use synthetic division to determine if the given value for \( k \) is a zero of this polynomial. If not, determine \( p(k) \).

\[ p(x) = 3x^4 - 13x^3 - 8x^2 + 75x - 45; k = 3 \]

Answer 6 Points

Selecting an option will display any text boxes needed to complete your answer.

Is \( k \) a zero of this polynomial?

• Yes
• No

Solution

To determine if \( k = 3 \) is a zero of the polynomial \( p(x) = 3x^4 - 13x^3 - 8x^2 + 75x - 45 \), we will use synthetic division. Write down the coefficients of the polynomial: \( 3, -13, -8, 75, -45 \). Set up synthetic division with \( k = 3 \). \[ \begin{array}{c|ccccc} 3 & 3 & -13 & -8 & 75 & -45 \\ & & 9 & -12 & -60 & 45 \\ \hline & 3 & -4 & -20 & 15 & 0 \\ \end{array} \] Bring down the leading coefficient: 3 Multiply by \( k = 3 \) and add: \( 3 \times 3 = 9 \), \(-13 + 9 = -4\) Multiply by \( k = 3 \) and add: \( -4 \times 3 = -12 \), \(-8 + (-12) = -20\) Multiply by \( k = 3 \) and add: \( -20 \times 3 = -60 \), \( 75 + (-60) = 15\) Multiply by \( k = 3 \) and add: \( 15 \times 3 = 45 \), \(-45 + 45 = 0\) Since the remainder is 0, \( k = 3 \) is a zero of the polynomial. The answer to the question “Is \( k \) a zero of this polynomial?” is Yes.