Question: An open-top box is to be constructed from a sheet of tin that measures 24 inches by 12 inches by…

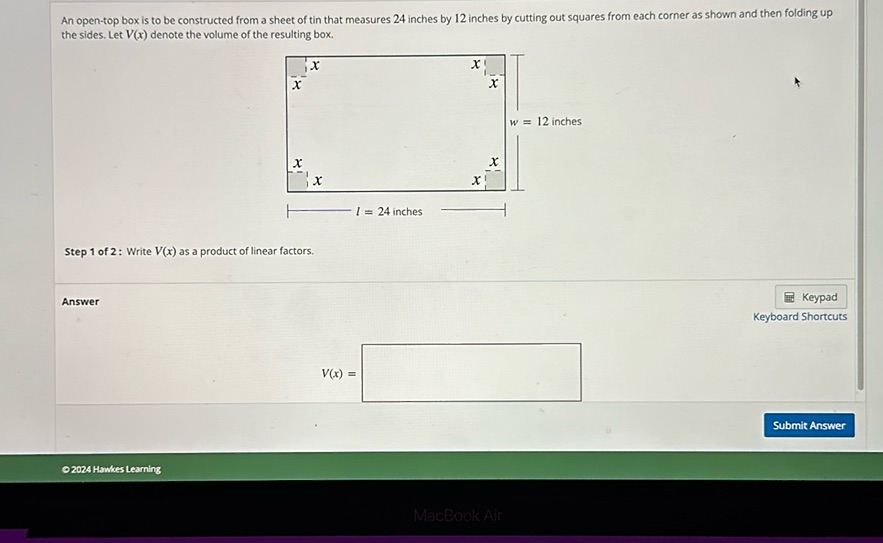
An open-top box is to be constructed from a sheet of tin that measures 24 inches by 12 inches by cutting out squares from each corner as shown and then folding up the sides. Let V(x) denote the volume of the resulting box.

[Diagram of a rectangle with dimensions 24 inches by 12 inches, showing squares of side length x cut out from each corner.]

Step 1 of 2: Write V(x) as a product of linear factors.

Answer

V(x) = [Blank space for answer]

Submit Answer

© 2024 Hawkes Learning

MacBook Air

Solution

Step 1: Identify the dimensions of the box after cutting out the squares. \[ V(x) = x(24 - 2x)(12 - 2x) \] Step 2: Factor out the common terms from each dimension. \[ V(x) = x \cdot 2(12 - x) \cdot 2(6 - x) \] Step 3: Simplify the expression by combining constants. \[ V(x) = 4x(12 - x)(6 - x) \]