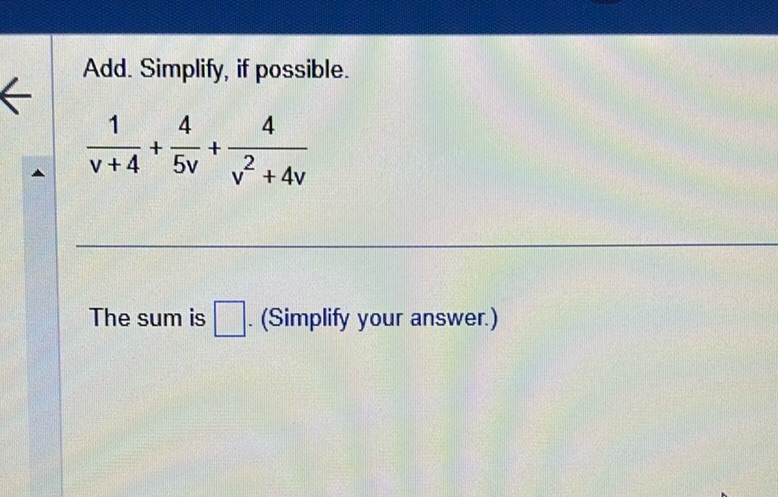
Question: Add. Simplify, if possible. \frac{1}{v+4} + \frac{4}{5v} + \frac{4}{v^2 + 4v} The sum is ____…

Add. Simplify, if possible.

\frac{1}{v+4} + \frac{4}{5v} + \frac{4}{v^2 + 4v}

The sum is ____. (Simplify your answer.)

Solution

Let’s simplify the expression step by step.

Find a common denominator.

\[ \text{LCM} = 5v(v + 4) & \]

Rewrite each fraction with the common denominator.

\[ \frac{1}{v+4} = \frac{5v}{5v(v + 4)} & \]

\[ \frac{4}{5v} = \frac{4(v + 4)}{5v(v + 4)} & \]

\[ \frac{4}{v^2 + 4v} = \frac{4}{v(v + 4)} = \frac{20}{5v(v + 4)} & \]

Add the fractions.

\[ \frac{5v + 4(v + 4) + 20}{5v(v + 4)} & \]

Simplify the numerator.

\[ 5v + 4v + 16 + 20 = 9v + 36 & \]

Factor the numerator.

\[ 9(v + 4) & \]

Cancel out the common terms.

\[ \frac{9(v + 4)}{5v(v + 4)} = \frac{9}{5v} & \]

The sum is \(\frac{9}{5v}\).